Which Mean? – Statsbook

Arithmetic mean

\( x_{arithmetic} = \frac{1}{n} \sum_{i=1}^{n} x_i \)

The arithmetic mean is the ‘normal’ mean and calculated by adding all observations together and then dividing by the total number of observations. The arithmetic mean gives a good estimate of central tendency in data that con be modelled with a normal distribution. However, it is very sensitive to outliers and not recommended for skewed data, where the median (middle value) is a better estimate of central tendency.

Data that can be modelled with a normal distribution are summarised with the mean (central tendency) and the standard deviation (spread).

Data that have a skewed distribution should be summarised using the median (central tendency) and the interquartile range (middle 50%).

Harmonic mean

\( x_{harmonic} = \frac{n}{ \sum_{i=1}^{n} \frac{1}{x_i} } \)

The harmonic mean is the reciprocal of the mean of the reciprocals as indicated in the formula above. This mean is better for ratios (ie speed).

For example, somebody drives 10 km at 20 km/hr and then the same 10 km back at 60 km/hr. What is the mean speed?

It is clearly NOT 40 km/hr (arithmetic mean)!

The first 10 km is at 20 km/hr: 10 km in 30 minutes

The return 10 km is at 60 km/hr: 10 km in 10 minutes

Consequently, the mean speed is 20 km in 40 minutes.

This is equal to 1/2 km a minute or 30 km/hr.

What is the harmonic mean:

\( x_{harmonic} = \frac{2}{ \frac{1}{20 } + \frac{1}{60} } = \frac{2}{\frac{4}{60}} = \frac{120}{4} = 30 km/hr \)

Similarly, let’s consider two surgeons. Surgeon A always does two operations per list and surgeon B (different speciality) always does six operations per list. If the number of lists is the same:

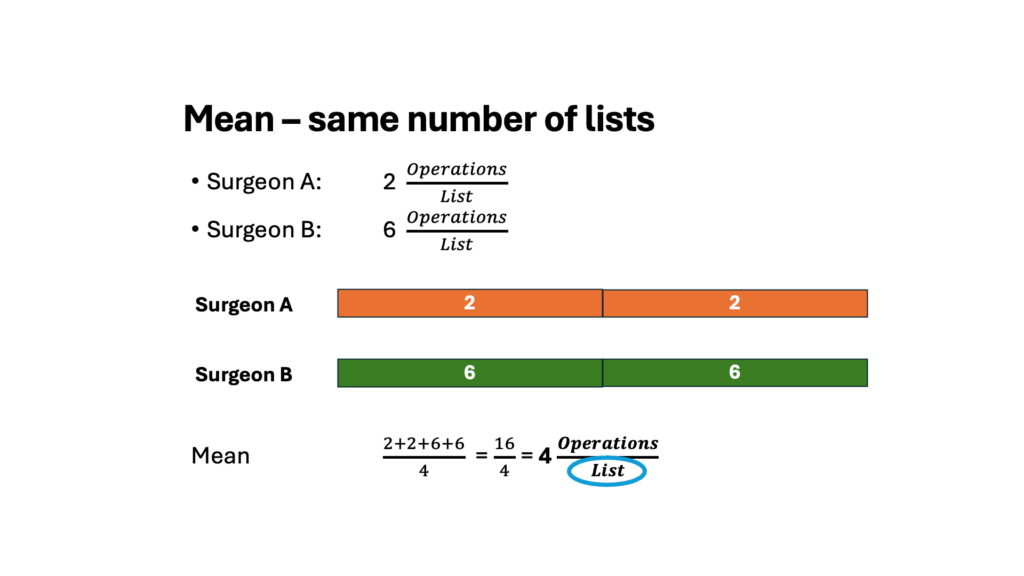
However, if the number of operations is the same:

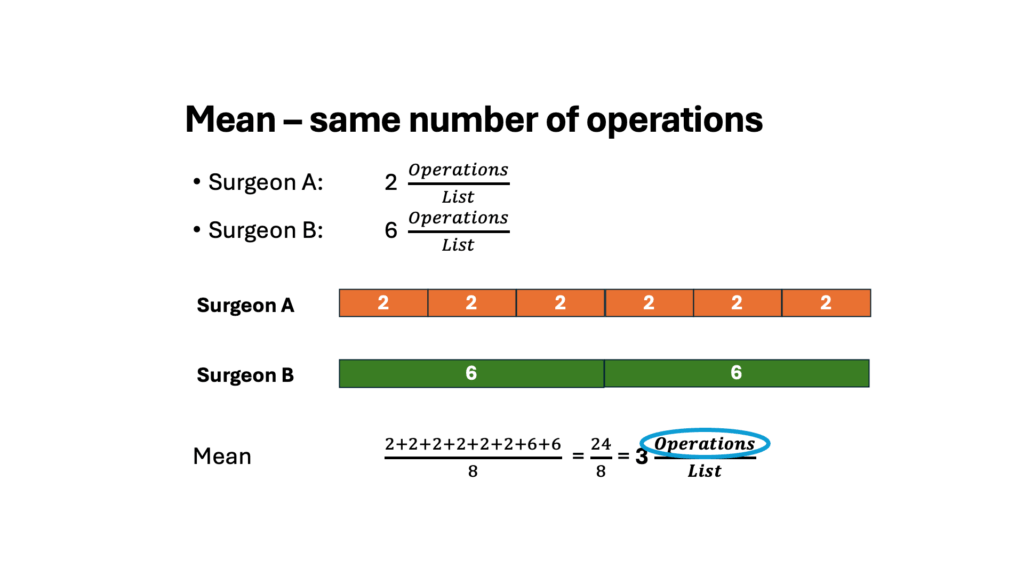
So, it depends what you are looking at what mean you require! If the number of operations is the same, the mean is 3 (harmonic mean, as the mean of the denominator is required). However, if the number of lists is the same, the mean is 4 (arithmetic mean, as dealing with the numerator)).

The harmonic mean of precision and recall (F1 score) is often used in machine learning to evaluate performance.

Geometric mean

\( x_{geometric} = \left( \prod_{i=1}^{n} x_i \right)^{\frac{1}{n}} = \sqrt[n]{ x_1 \cdot x_2 \cdot \cdots \cdot x_n } \)

This mean is used for multiplicative factors such as investment return rates, but also survival probabilities. The geometric mean gives an overall average survival probability across survival times, emphasising the multiplicative (cumulative) nature of survival probabilities.

For example if the survival at:

year 1 is 0.9
year 2 0.81
year 3 0.72

\(x_{geom} = \sqrt[3]{ 0.9 \cdot 0.81 \cdot 0.72 } = \sqrt[3]{ 0.52488 } \approx 0.807\)

The arithmetic mean and harmonic mean of the same numbers are:

\(x_{arithmetic} = \frac{ 0.9 + 0.81 +0.72 }{3} = 0.81 \)

\( x_{harmonic} = \frac{3}{ \frac{1}{0.9 } + \frac{1}{0.81} + \frac{1}{0.72} } \approx 0.803 \)

The arithmetic mean is always larger than the geometric mean and the geometric mean is always larger than the harmonic mean.

Quadratic mean (Root Mean Square)

\( x_{rms} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2} \)

The quadratic mean is better known as the root mean square and is used to find a magnitude of time varying data (for example alternating current, electrical signals in electro-cardiogram / electro-encephalogram, electro-myogram). In addition, the root mean square is useful in estimating uncertainty in repeated measurements. It is also used in machine learning to evaluate performance of for example regression models. Using the same numbers as above:

\( x_{rms} = \sqrt{0.9^2 + 0.81^2 + 0.72^2} \approx 1.41 \)