Life table analysis is mostly obsolete in orthopaedics and Kaplan-Meier survival analysis is the preferred method as the exact failure time is usually known. Two variables are required:
- Follow up time (continuous variable)
- Censor (end point, nominal dichotomous variable
- yes / no , 0 / 1
An optional grouping variable to compare different groups:
- Grouping (nominal grouping variable)
Often the follow up time and censor need to be calculated from dates. In this respect the script survivaldates may be useful (this is an example script on how to convert dates to follow up time and how to create the censor variable; use survivaldates.rda with this example). Alternatively, spreadsheet programs can be used to calculate the follow up time from dates.
The censor is a dichotomous variable as each patient can only in one of two states: uncensored or censored. Once the event of interest has occurred, the patient is uncensored. All other patients are censored. Patients can be censored due to :
- The event has not occurred before the end of the study
- The patient is lost to follow up during the study
- The patient withdraws from the study due to another reason (i.e. death if the event of interest is failure of hip replacement)
Before survival analysis can be performed, the data needs to be in an appropriate format. The data should be in a table with as many rows as there are patients. There should be at least two columns; a column for the continuous follow up variable and a column for the binary censor variable (0 or 1). A third categorical grouping column is optional, but can be used to compare different groups of patients.
Here, the plotsurvival.rda dataset is used with several methods on how to perform the analysis similar, but more in depth as described on the surival plot page. The methods described are:
- Console method
- KM with Numbers function
- Prodlim package
Console method
The survival package1 should be installed and active.
library(survival)To check the data frame is loaded:
plotsurvival
number fu group censor
1 1 5.2 Hip 1 0
2 2 6.3 Hip 1 0
3 3 7.0 Hip 1 0
4 4 8.5 Hip 1 0
5 5 9.4 Hip 1 0
6 6 10.1 Hip 1 0
7 7 11.2 Hip 1 0
8 8 12.0 Hip 1 0
9 9 12.5 Hip 1 1
10 10 12.7 Hip 1 0
11 11 4.5 Hip 2 1
12 12 5.8 Hip 2 0
13 13 6.9 Hip 2 0
14 14 7.8 Hip 2 1
15 15 8.2 Hip 2 1
16 16 8.9 Hip 2 1
17 17 9.5 Hip 2 1
18 18 10.2 Hip 2 0
19 19 11.5 Hip 2 0
20 20 12.9 Hip 2 0To perform survival analysis for all hips together, first create a survival object and call this mysurvival:
mysurvival <- Surv(plotsurvival$fu,plotsurvival$censor)To show the object:
mysurvival
[1] 5.2+ 6.3+ 7.0+ 8.5+ 9.4+ 10.1+ 11.2+ 12.0+ 12.5 12.7+ 4.5 5.8+ 6.9+ 7.8 8.2 8.9 9.5 10.2+ 11.5+ 12.9+This shows the survival times of all patients. The follow up times followed by a ‘+’ are censored; the others have failed.
A summary of the object can be useful:
summary(mysurvival)
time status
Min. : 4.500 Min. :0.0
1st Qu.: 6.975 1st Qu.:0.0
Median : 9.150 Median :0.0
Mean : 9.055 Mean :0.3
3rd Qu.:11.275 3rd Qu.:1.0
Max. :12.900 Max. :1.0 So the shortest follow time is 4.5 years and the longest 12.9 years, with a median follow up time of 9.15 years.
Next, a Kaplan-Meier (product limit) survival curve, called mycurve, is fitted on the mysurvival object (without confidence interval):
mycurve <- survfit(mysurvival~1, conf.int=FALSE)Please note the tilde 1 (~1). This is a required grouping parameter. If there are no groups, it should be set to 1.
To show the survival estimate:
mycurve
Call: survfit(formula = mysurvival~1, conf.int=FALSE)
n events median
[1,] 20 6 12.5So, there are 20 patients of whom 6 failed (event). The median survival is the time it takes for the cumulative survival to become 50%. Here, the median survival is 12.5 years.
A more detailed summary can be useful:
summary(mycurve)
Call: survfit(formula = mysurvival ~ 1, conf.int = FALSE)
time n.risk n.event survival std.err
4.5 20 1 0.950 0.0487
7.8 14 1 0.882 0.0795
8.2 13 1 0.814 0.0982
8.9 11 1 0.740 0.1138
9.5 9 1 0.658 0.1275
12.5 3 1 0.439 0.1982It is easy to obtain a survival probability at a specified time. For example, the survival probability at 5 years is:
summary(mycurve,time=5)
Call: survfit(formula = mysurvival ~ 1, conf.int = FALSE)
time n.risk n.event survival std.err
5 19 1 0.95 0.0487or 49%; and the survival probability at 10 years is:
summary(mycurve,time=10)
Call: survfit(formula = mysurvival ~ 1, conf.int = FALSE)
time n.risk n.event survival std.err
10 8 5 0.658 0.127or 13%.
To show the survival curve:
plot(mycurve, conf.int=FALSE, mark.time=TRUE)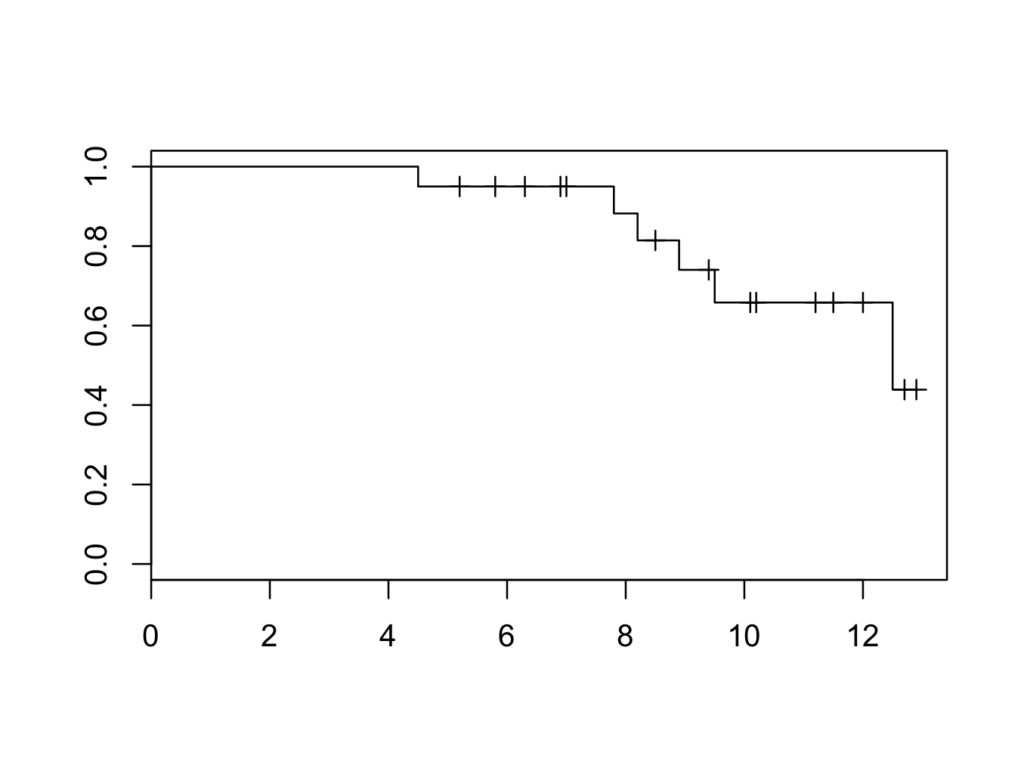
mark.time=TRUE adds the censor tick marks to the plot (default = FALSE)
and add axes labels:
title(main='KM curve', xlab='Follow Up [years]',ylab='Probability')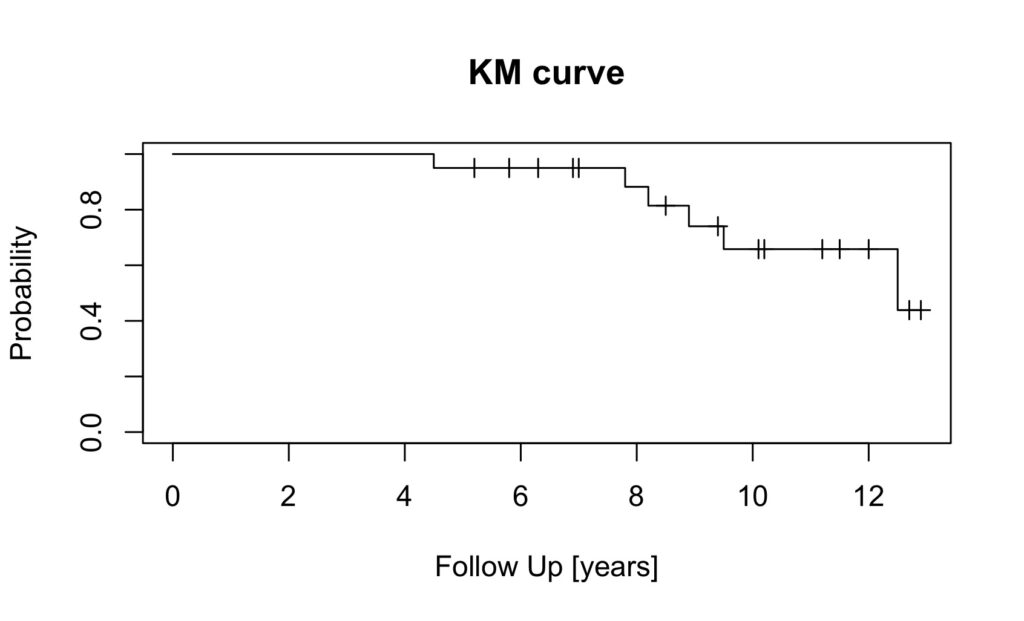
The censored patients are indicated by a tick mark on the survival curve. To create the plot in a different colour is easy:
plot(mycurve,col='salmon', conf.int=FALSE, mark.time=TRUE)
title(main='KM curve', xlab='Follow Up [years]',ylab='Probability')
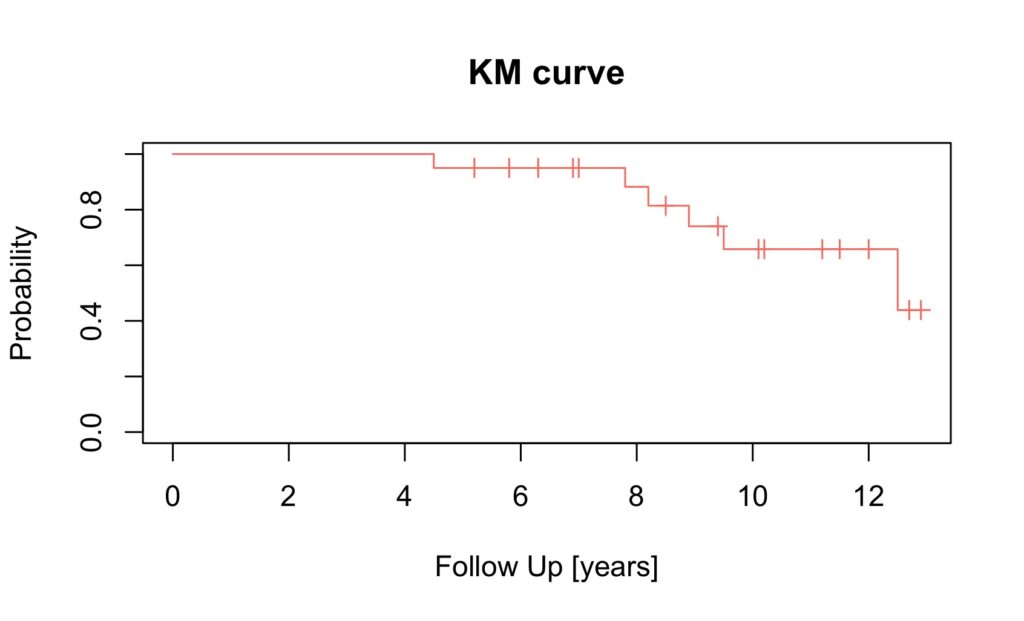
For a full list of available colours:
colors() Output omitted for brevity.
Please note the American spelling of color
To add a confidence interval to the survival curve is also straight forward and should be included in the mycurve object:
mycurve <- survfit(mysurvival~1, conf.int=0.95)
summary(mycurve)
Call: survfit(formula = mysurvival ~ 1, conf.int = 0.95)
time n.risk n.event survival std.err
4.5 20 1 0.950 0.0487
7.8 14 1 0.882 0.0795
8.2 13 1 0.814 0.0982
8.9 11 1 0.740 0.1138
9.5 9 1 0.658 0.1275
12.5 3 1 0.439 0.1982
lower 95% CI upper 95% CI
0.859 1.000
0.739 1.000
0.643 1.000
0.548 1.000
0.450 0.962
0.181 1.000The confidence interval level can be changed by altering the conf.int value.
To plot a ‘slategray’ curve with 95% confidence intervals:
plot(mycurve,col='slategray', mark.time=TRUE)
title(main='KM curve', xlab='Follow Up [years]',ylab='Probability')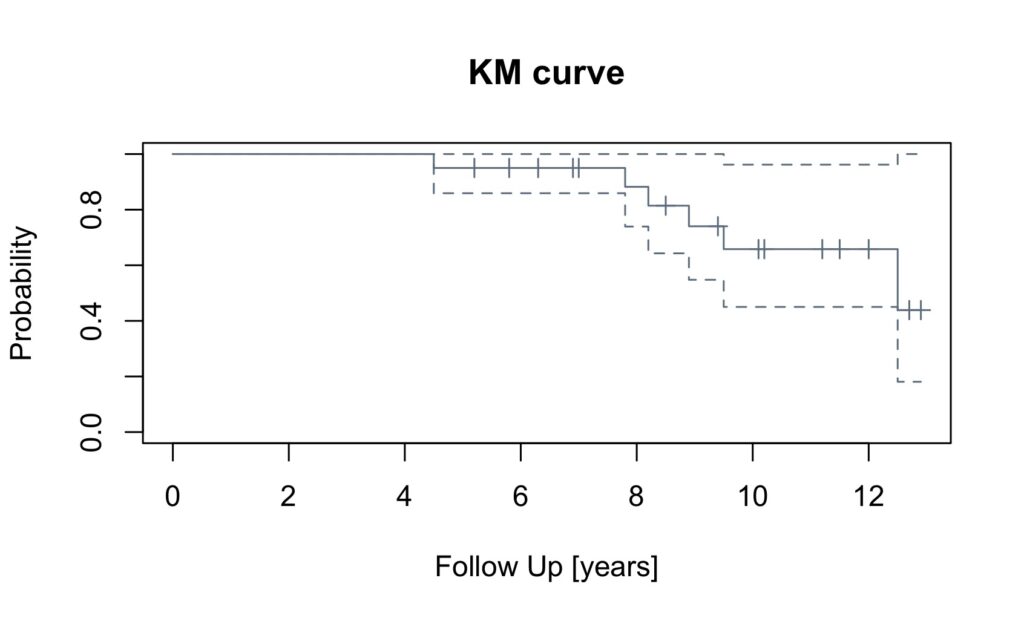
Create a survival object similar as to described above. However, in the Kaplan Meier estimate object, set the grouping variable after the tilde (~) sign (here the categorical ‘group’ variable in the ‘plotsurvival’ data frame).
library(survival)
mysurvival<-Surv(plotsurvival$fu,plotsurvival$censor)
mysurvival
[1] 5.2+ 6.3+ 7.0+ 8.5+ 9.4+ 10.1+ 11.2+ 12.0+ 12.5 12.7+ 4.5 5.8+ 6.9+ 7.8 8.2 8.9 9.5 10.2+ 11.5+ 12.9+
mycurve=survfit(mysurvival~plotsurvival$group, conf.int=FALSE)
mycurve
Call: survfit(formula = mysurvival ~ plotsurvival$group, conf.int = FALSE)
n events median
plotsurvival$group=Hip 1 10 1 12.5
plotsurvival$group=Hip 2 10 5 9.5
summary(mycurve)
Call: survfit(formula = mysurvival ~ plotsurvival$group, conf.int = FALSE)
plotsurvival$group=Hip 1
time n.risk n.event survival std.err
12.500 2.000 1.000 0.500 0.354
plotsurvival$group=Hip 2
time n.risk n.event survival std.err
4.5 10 1 0.900 0.0949
7.8 7 1 0.771 0.1442
8.2 6 1 0.643 0.1679
8.9 5 1 0.514 0.1769
9.5 4 1 0.386 0.1732Now plot the curves with labels to the axes and a title:
plot(mycurve, col=c('wheat','green'), mark.time=TRUE)
title(main='KM curve', xlab='FU [years]', ylab='Probability') 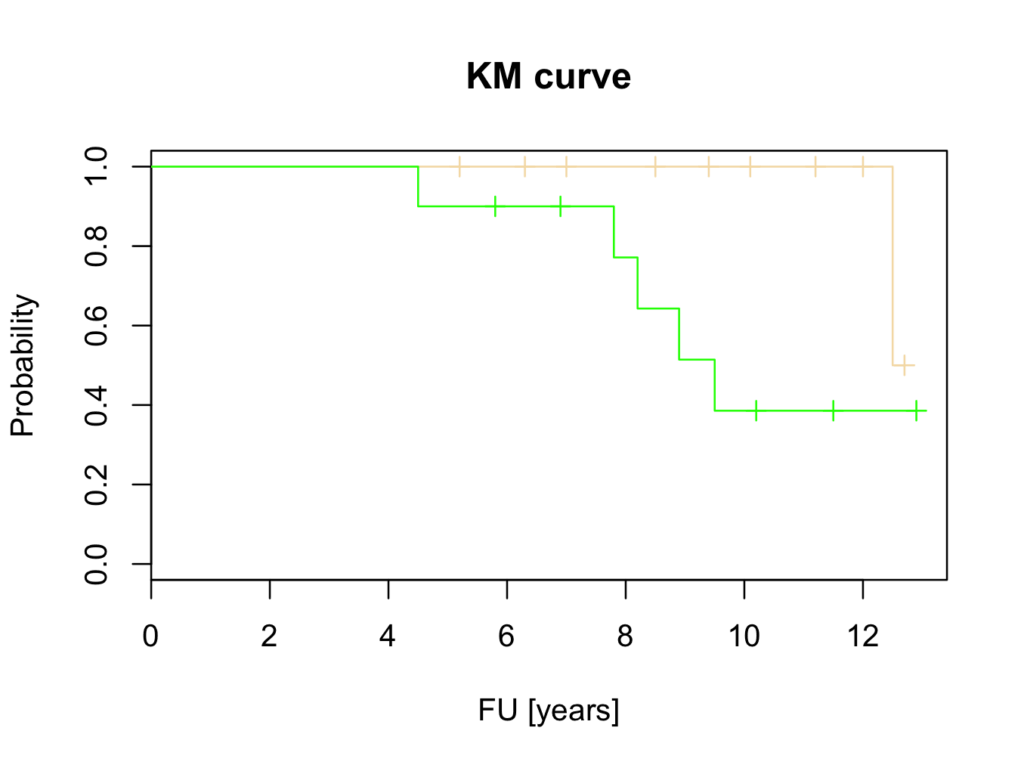
This suggests that Hip 1 is superior to Hip 2. However, this will be tested with the logrank test, Cox proportional hazards and parametric tests.
Please note Hip 1 has a survival of 100% until there is a significant drop at the end. Only two patients had a follow up beyond 11 years.
Logrank test
The log rank test is a test that compares two survival curves. The null hypothesis is that the curves are identical. The statistical method uses a Chi Square test in its calculation. To perform this test in R is straight forward. The function that does the test is called “survdiff” (survival difference). Previously, the survival object was defined as mysurvival, but it is redefined (just in case) and its contents checked:
mysurvival <- Surv(plotsurvival$fu, plotsurvival$censor)
mysurvival
[1] 5.2+ 6.3+ 7.0+ 8.5+ 9.4+ 10.1+ 11.2+ 12.0+ 12.5 12.7+ 4.5 5.8+ 6.9+ 7.8 8.2 8.9 9.5 10.2+ 11.5+ 12.9+To perform the log rank test:
mylogrank <- survdiff(mysurvival~plotsurvival$group)
mylogrank
Call:
survdiff(formula = mysurvival ~ plotsurvival$group)
N Observed Expected (O-E)^2/E (O-E)^2/V
plotsurvival$group=Hip 1 10 1 3.31 1.61 3.63
plotsurvival$group=Hip 2 10 5 2.69 1.97 3.63
Chisq= 3.6 on 1 degrees of freedom, p= 0.06The p value is larger than 5% and therefore the null hypothesis can’t be rejected. Although the curve suggests that Hip 2 performs worse than Hip 1, this can’t be confirmed statistically. However, there were only 10 patients in each group and the test lacks statistical power. Perhaps a more powerful test can show a difference (such as Cox proportional hazards or a parametric test; see below)?
Cox proportional hazards
The cox proportional hazards test is a non parametric test that compares two or more survival curves. It is commonly used in medicine and more powerful than the log rank test. The function that performs this test in R is called “coxph”. The test is performed on the previously defined mysuvival object and the syntax is very similar to the log rank test:
mycoxproportionalhazards <- coxph(mysurvival~plotsurvival$group)
mycoxproportionalhazards
Call:
coxph(formula = mysurvival ~ plotsurvival$group)
coef exp(coef) se(coef) z p
plotsurvival$groupHip 2 1.837 6.275 1.100 1.669 0.0951
Likelihood ratio test=3.84 on 1 df, p=0.04996
n= 20, number of events= 6 The Cox proportional hazard test shows a statistical significant difference. Therefore, the Cox proportional hazards test rejects the null hypothesis in favour of the alternate hypothesis and it is concluded that Hip 1 outperforms Hip 2. Please refer to the section on Cox proportional hazards for more information about this linear regression model.
Parametric
Parametric regression analysis can also be used to compare different survival curves. This method is more powerful than the methods describe above. However, it makes assumptions about the shape of the hazard function, which may or may not be justified. Assumptions of different types of hazard curves include (amongst others):
- Constant hazard (“exponential”)
- a constant hazard gives an exponential distribution.
- Increasing hazard
- hazard increases as time goes on.
- Decreasing hazard
- hazard decreases as time goes on.
The R function ‘survreg’, that performs parametric regression analysis on survival curves, includes attributes for several distributions. These include: ‘weibull’, ‘exponential’, ‘gaussian’, ‘logistic’,’lognormal’ and ‘loglogistic’. A full description is outside the scope of this book. Further information can be obtained from the build in help function. To perform regression analysis on the example is similar to the other tests and based on the mysurvival object:
Model 1: assume a constant hazard (exponential distribution):
myexponential <- survreg(mysurvival~plotsurvival$group,dist='exponential')
myexponential
Call:
survreg(formula = mysurvival ~ plotsurvival$group, dist = "exponential")
Coefficients:
(Intercept) plotsurvival$groupHip 2
4.552824 -1.705591
Scale fixed at 1
Loglik(model)= -24.8 Loglik(intercept only)= -26.4
Chisq= 3.31 on 1 degrees of freedom, p= 0.0689
n= 20 So, if a constant hazard is assumed, p>5% and the null hypothesis can’t be rejected. It must be concluded that there is no difference between the two hips. However, it is unlikely that the hazard remains constant over time. It is much more likely that the hazard for aseptic loosening increases over time. Therefore, it seems more appropriate to use a model such as Weibull:
Model 2: Weibull, increasing hazard over time:
myweibull <- survreg(mysurvival~plotsurvival$group,dist='weibull')
myweibull
Call:
survreg(formula = mysurvival ~ plotsurvival$group, dist = "weibull")
Coefficients:
(Intercept) plotsurvival$groupHip 2
2.9364589 -0.5055782
Scale= 0.2617896
Loglik(model)= -20 Loglik(intercept only)= -22.2
Chisq= 4.31 on 1 degrees of freedom, p= 0.0378
n= 20 The Weibull model is statistical significant and the null hypothesis can be rejected in favour of the alternate hypothesis. It can be concluded that Hip 1 is better than Hip 2 when the Weibull model is used.
Cox proportional hazards or parametric regression analysis?
Both, parametric and non parametric analysis may be appropriate to use to demonstrate a difference between two groups. Parametric regression analysis is more powerful, but makes assumptions regarding the shape of the hazard function. This may not always be appropriate. Parametric regression analysis defines the shape of the hazard function and therefore allows for extrapolation. This is not possible with the Cox proportional hazards model.
Traditionally, medical studies tend to use the Cox proportional hazards model whilst engineering uses the parametric regression analysis. However, parametric analysis can easily be applied to medicine and this can be particularly useful if prediction / extrapolation is required.
Hazard plot
This function requires the muhaz2 package to be installed and loaded. The hazard function is related to the survival function and can be derived from it. Given the patient has survived up to a certain time, the hazard function gives the instantaneous hazard for the event to happen at that time. Hazard plots can be very useful in estimating the risk of the event of interest occurring, given the patient has survived up to that time. Still using the same example, the muhaz function from the muhaz package does this conveniently. Enter the following in the R command window:
library(muhaz)
myhazard <- muhaz(plotsurvival$fu, plotsurvival$censor, max.time=4)
plot(myhazard)
title(main='Hazard Plot')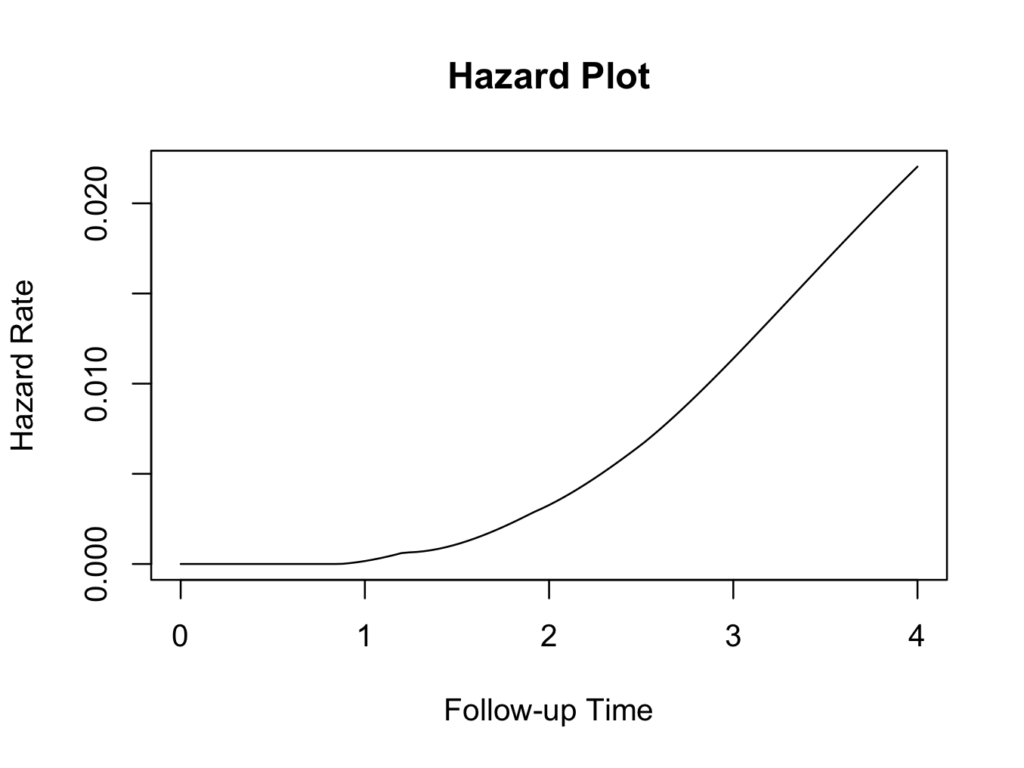
The plot shows that the hazard of failure increases over time, suggesting that it would be appropriate to use the parametric Weibull analysis as described above.
Kaplan-Meier plot showing numbers at risk
It may be preferable to have the number of patients at risk indicated in the plot. The KMatRisk function can be used for this. Copy the function to the clipboard, paste it into the console and hit return. The function should now be available in R (the library survival3 should also be installed and loaded).
Create the survival curve object directly (in one step) from the data and call this hipfit:
hipfit <- survfit(Surv(fu,censor)~group, data=plotsurvival)Next call the loaded function to create the survival curve with numbers at risk:
ggkm(hipfit,timeby=1,ystratalabs=c("Hip 1","Hip 2"),main="KM plot, Hip by type",xlabs="FU [Years]")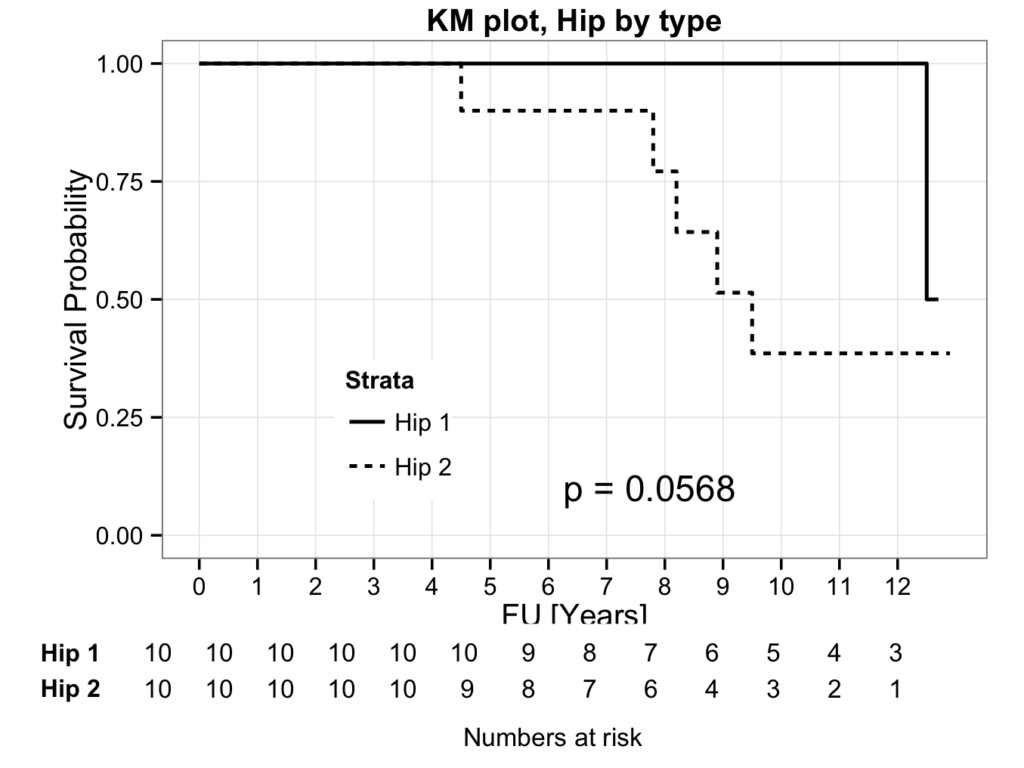
Prodlim package
The prodlim4 package should be installed. The package creates nice survival curves. First load the package:
library(prodlim)Create a Kaplan-Meier object (called kmhipfit) using the product limit method:
kmhipfit <- prodlim(Hist(fu, censor) ~ 1, data = plotsurvival)To create a plot that shows numbers at risk at yearly intervals with a shadowed 95% confidence interval:
plot(kmhipfit, percent=FALSE, axes=TRUE, axis1.at=seq(0,kmhipfit$maxtime+1,1), axis1.lab=seq(0,kmhipfit$maxtime+1,1), marktime=TRUE, xlab="Years", atrisk=TRUE, atrisk.labels="At Risk:", confint=TRUE, confint.citype="shadow", col=4)And add a title:
title(main= "Kaplan Meier Survival Analysis - All Hips")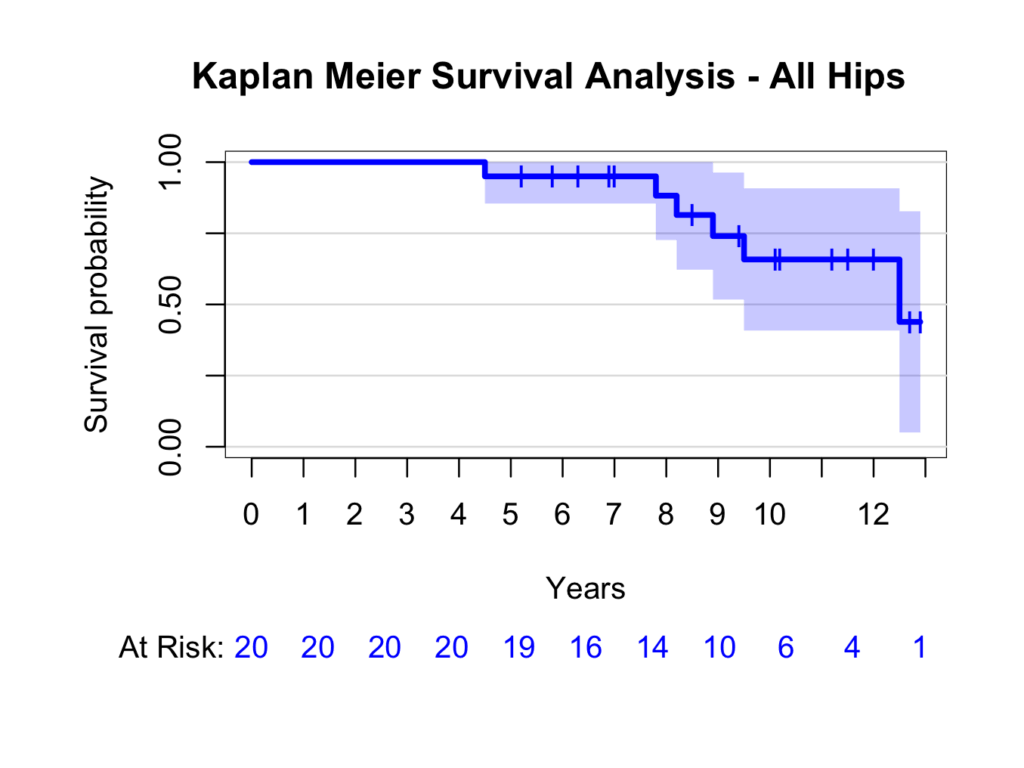
Similarly, create a plot grouped by type of hip replacement (instead of ~1, use ~group):
kmhipfit2 <- prodlim(Hist(fu, censor) ~ group, data = plotsurvival)
plot(kmhipfit2,percent=FALSE, axes=TRUE, axis1.at=seq(0,kmhipfit2$maxtime+1,1), axis1.lab=seq(0,kmhipfit2$maxtime+1,1), marktime=TRUE,xlab="Years", atrisk=TRUE, atrisk.labels="At Risk:", confint=TRUE, confint.citype="shadow", col=c(4,3), legend=TRUE, legend.x=0, legend.y=0.4, legend.cex=1)
title(main= "Kaplan Meier Survival Analysis - By Hip Type")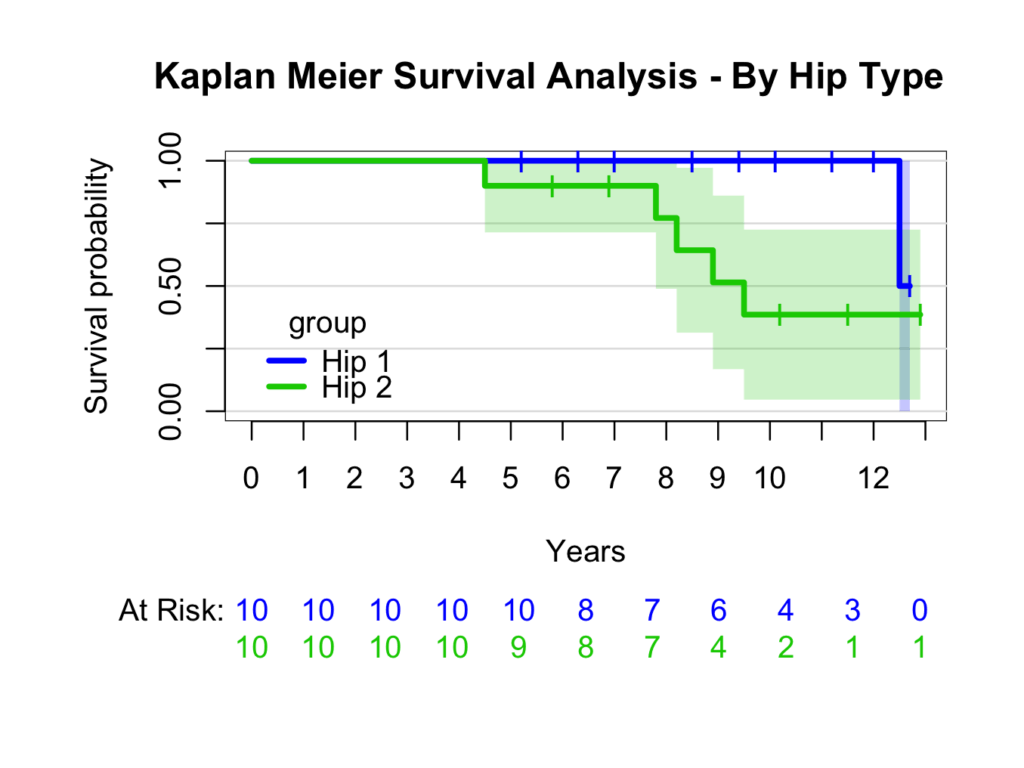
Please note the syntax to place the legend position.
For more information re prodlim options:
??prodlim
Other packages that can be of use in creating survival curves are the survminer5 and the ggfortify 6 packages (autoplot() function) that are designed to work with ggplot27. For examples please refer to the survival plot page.