Statsbook

Other Models

As described, a regression line was fitted through 30 data points in the trees30.rda data set. Data were also extrapolated and it was estimated that a tree with a diameter of 500 centimetres would have a mass of 1208 kilogram. However, one should be more cautious when extrapolating data as is illustrated below. The data set has been extended and the data of 104 trees can be found in trees.rda. The data is shown by:

ExtendedTreeGirthMass 
    Girth Mass
1     205  251
2     213  272
.....
.....
103   522 2508
104   527 2375

The formula of the line is found by:

fit<-lm(Mass~Girth,data=ExtendedTreeGirthMass)
fit
Call:
lm(formula = Mass ~ Girth, data = ExtendedTreeGirthMass)
Coefficients:
(Intercept)        Girth  
  -1225.413        5.874 

The equation of the line therefore is:

\(Mass = 5.874 \cdot Girth – 1225.413 \)

Please note the equation of this line is different from the one found when there were only 30 trees in the data set (Mass = 3.24×Girth -411.62).

The correlation coefficient is found by:

cor(ExtendedTreeGirthMass$Mass,ExtendedTreeGirthMass$Girth,method='pearson')
[1] 0.916265

A correlation coefficient of 92% does appear very satisfactory. However, if we plot the data, the fit is perhaps somewhat disappointing:

ggplot(data=ExtendedTreeGirthMass,aes(x = Girth,y = Mass)) + 
geom_point() + 
ggtitle(label = "Girth and Mass Trees") + 
xlab(label = "Girth [cm]") + 
ylab(label = "Mass [kg]") + 
geom_smooth(method = 'lm') + 
theme_bw()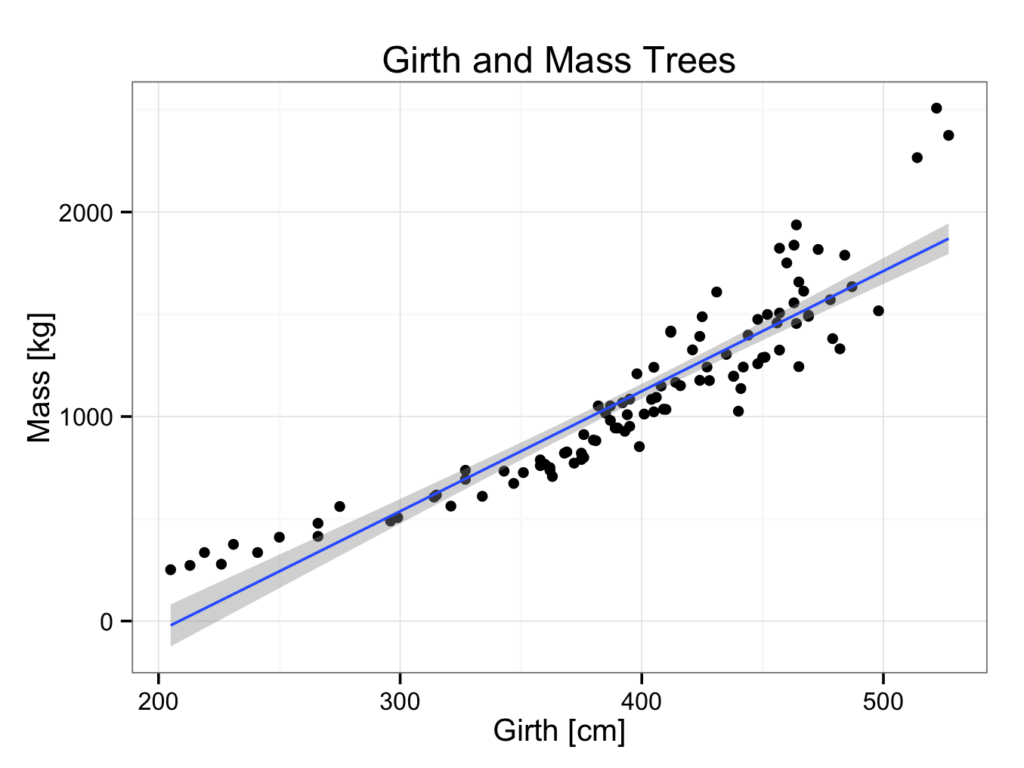

Looking at the plot, it seems an exponential relation seems more appropriate. This would also fit our understanding of growth better. This is another example why it is always advisable to plot the data and not only rely on descriptive values.

To fit an exponential regression line to the data, use the equation:

\(y = b \cdot e^{a \cdot {x}} \)
\(Mass = b \cdot e^{a \cdot{Girth}} \)
\( log(Mass) = log(b \cdot e^{a \cdot {Girth}}) \)
\(log(Mass) = log(b) + a \cdot {Girth} \)
\(log (Mass) = c + a \cdot {Girth} \)

There are two ways to perform exponential curve fitting:

1 Transform the y axis to logarithmic scale:

ggplot(data=ExtendedTreeGirthMass, aes(x = Girth,y = Mass)) + 
geom_point() + 
ggtitle(label = "Girth and Mass Trees") + 
xlab(label = "Girth [cm]") +
ylab(label = "Mass [kg]") +
geom_smooth(method = 'loess') +
coord_trans(y = "log10") +
theme_bw()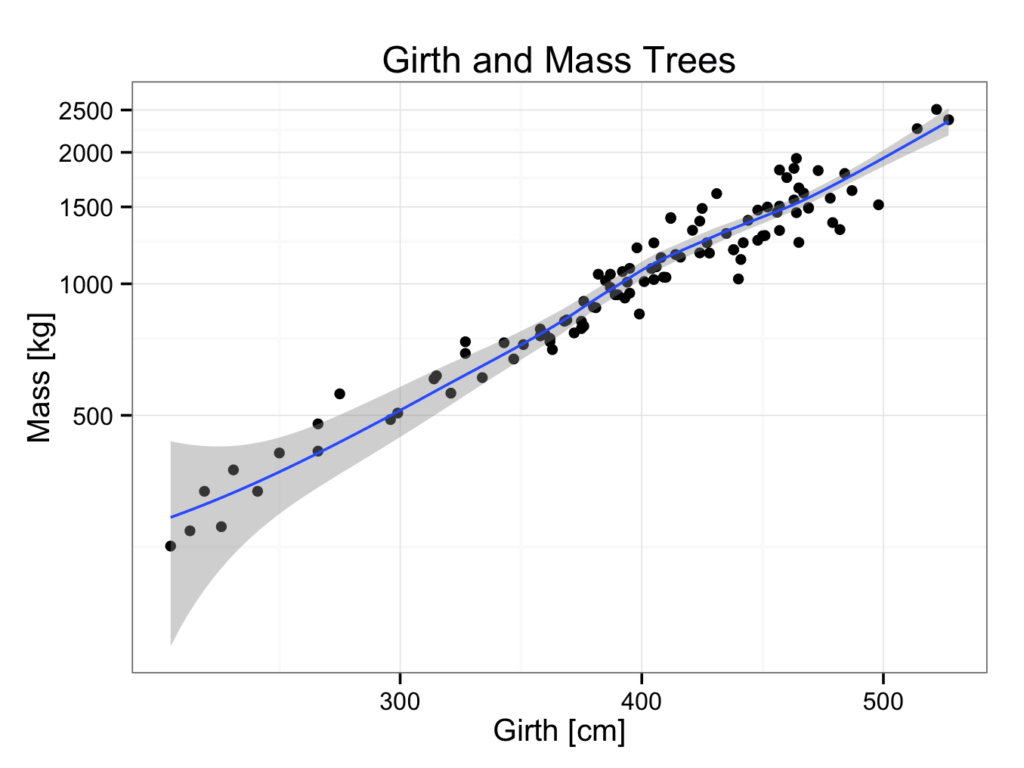

The advantage of this method is that it is very straight forward and that the original values on the axes are maintained. However, it is difficult to obtain the equation of the logarithmic regression analysis and perform inter- or extrapolation. Furthermore, the linear model gives data out of range and therefore a loess (smooth) model is required (resulting in a line that is not straight).

Please note to use loess and not lm (linear model) as method!

2 Log tranformation:

ggplot(data=ExtendedTreeGirthMass, aes(x = Girth,y = log(Mass))) + 
geom_point() + 
ggtitle(label = "Girth and Mass Trees") +
xlab(label = "Girth [cm]") +
ylab(label = "log(Mass [kg])") +
geom_smooth(method = 'lm') +
theme_bw()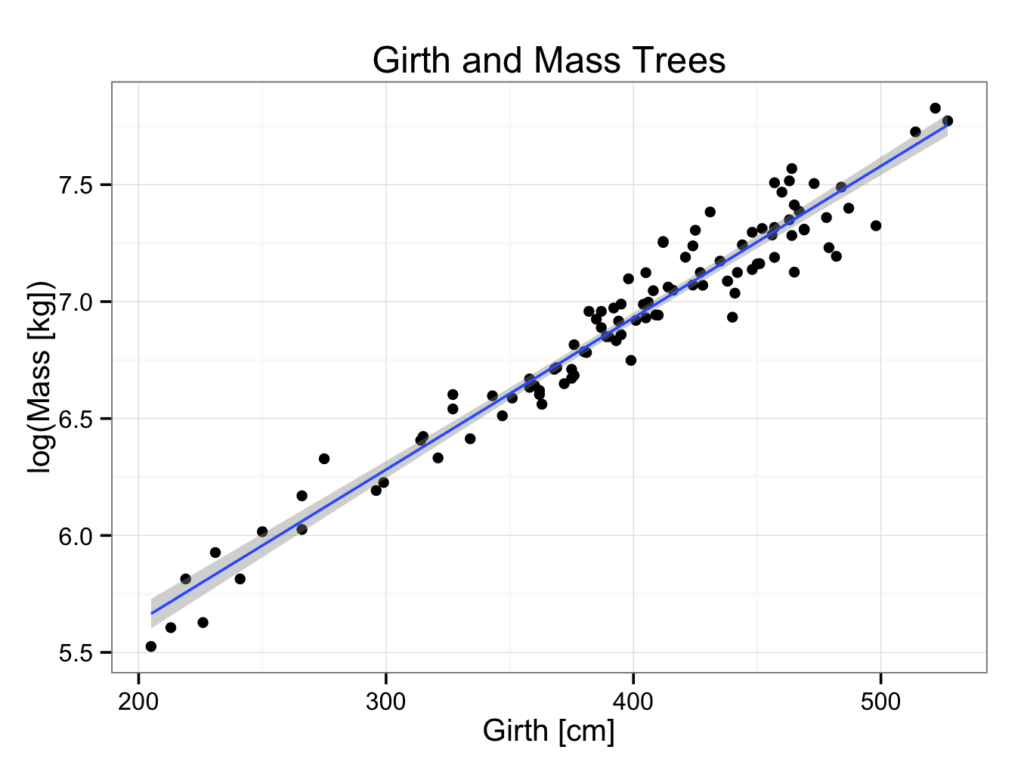

The original (untransformed) values are indicated on the x-axis, but transformed values on the y axis, making interpretation perhaps more difficult.

To find the equation of the logarithmic regression line:

fit <- lm(log(Mass)~Girth,data=ExtendedTreeGirthMass)
fit
Call:
lm(formula = log(Mass) ~ Girth, data = ExtendedTreeGirthMass)
Coefficients:
(Intercept)        Girth  
    4.33456      0.00649 

The formula of the logarithmic regression line therefore is:

\(Log(Mass) = 0.00649 \cdot Girth + 4.33456 \)

Extrapolation with linear and log model

Using the linear model, a tree with a girth of 500 centimetres would have a mass of:

\(Mass=5.874 \cdot 500-1225.413 \approx 1712 kg \)

However, using the log model:

\(Log(Mass)=0.00649 \cdot 500 + 4.33456 =7.57956 \)

Mass ≈ 1958 kg

The prediction with the logarithmic model fits the data much better.