Parametric tests can only be used if the data conform a Normal distribution (or any other known distribution). Therefore, the data need to be continuous. However, not all continuous data conform to a Normal distribution and data could well be skewed.
Often, we do not know how data are distributed and it is difficult to tell from our sample what the distribution of data is. The distribution could be Normal; but we are not sure. It this case we can use a statistical test to test whether the data is normally distributed or not. There are several test described to test for Normality. Examples include the Shapiro-Wilk test, Kolmogorov-Smirnov test and Quantile-Quantile plots.
Provided data are Normally distributed and the sample size is large (>50) we can use the Normal distribution itself and read from the graph. Usually, we perform a two sided test. This means that the alternate hypothesis could be bigger or smaller than the null hypothesis. Consequently, we have to ‘share’ the 5% between the two tail ends of the curve (2.5% at each tail end):
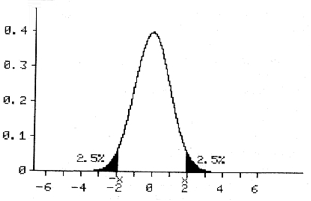
It should be noted that this is plus or minus twice the standard deviation from the mean. So, if the value of the test statistic lies in each of the two dark areas on the graph; we feel this is very unlikely to be due to chance and the null hypothesis is rejected in favour of the alternate hypothesis.
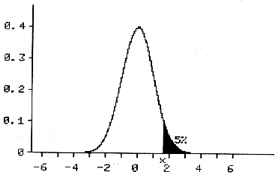
Occasionally, it is appropriate to do one sided testing:
t-Test
If the sample size is large (> 50), we can use the Normal distribution and read from graphs / tables. However, it is unusual to have such large sample sizes and often sample sizes are much smaller (around 20 to 30).Consequently, a ‘correction’ has to be made for the small sample size. This can be done using the t-test.
As example we use the skinfold.rda data on the thickness of the skinfold in patients with and without cancer. For now, let us assume we have demonstrated that it is reasonable to model the data with a Normal distribution (test for Normality) and the t-test can be used to analyse the data. A mathematical description of the t-test is beyond the scope of this book. Suffice to say that the t-test corrects for the smaller sample size with a ‘correction factor’.
To perform a t-test it is necessary to have a continuous outcome variable and a nominal grouping variable.
To perform an unpaired t-test (a paired t-test would be before and after a treatment; so the data are paired)in R:
t.test(Skinfold~Group,data=skinfold)
Welch Two Sample t-test
data: Skinfold by Group
t = -2.7653, df = 26.968, p-value = 0.01013
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.0475746 -0.4513143
sample estimates:
mean in group Cancer mean in group No Cancer
2.955556 4.705000 The computer calculates the p value using the t-test:
p = 0.010
Therefore, the probability that the test statistic takes a more extreme value is very small and unlikely due to chance (statistically significant). Consequently, the null hypothesis is rejected in favour of the alternate hypothesis. It is concluded that there is a difference in skin fold thickness in patients with cancer and that their nutrition is poorer.
In the example above, the t-test was performed on unpaired data. A t-test can also be performed on paired samples; before and after an intervention or treatment. If the data are dependent / related, use a paired t-test. Otherwise, use an unpaired t-test. An example of dependent data is the range of movement in the knee before and after a total knee replacement. We have two groups of data: range of movement before and after total knee replacement. The two groups are dependent and provided the data conform a Normal distribution; it is reasonable to use a paired t-test.
Back to the example; on the basis of the t-test, it seems reasonable to reject the null hypothesis (there is no difference in skinfold thickness between cancer and non cancer patients) in favour of the alternate hypothesis and conclude that there is a difference in skinfold thickness (and therefore nutritional status). However, we may not have been correct in using a t-test, as it has not been demonstrated the data can reasonably be modelled with a Normal distribution. To check Normality of all the skinfold thickness data:
shapiro.test(skinfold$Skinfold)
Shapiro-Wilk normality test
data: skinfold$Skinfold
W = 0.8519, p-value = 0.0008328Please note the capital S in the Skinfold variable within the skinfold data frame (with lower case s)
The p value is significant, suggesting the data can’t be modelled with a Normal distribution. However, only the data of both groups together (Cancer and Non Cancer) has been examined for Normality. But we have just demonstrated there is a statistical difference between the two groups and they are not likely to belong to the same distribution (p<0.05)! In addition, Normality should be tested in both groups separately:
shapiro.test(skinfold$Skinfold[which(skinfold$Group =='No Cancer')])
Shapiro-Wilk normality test
data: skinfold$Skinfold[which(skinfold$Group == "No Cancer")]
W = 0.8856, p-value = 0.0223and
shapiro.test(skinfold$Skinfold[which(skinfold$Group =='Cancer')])
Shapiro-Wilk normality test
data: skinfold$Skinfold[which(skinfold$Group == "Cancer")]
W = 0.8047, p-value = 0.02309The [which(skinfold$Group ==’No Cancer’)] part only selects the ‘No Cancer’ patients from the data frame
In addition, quantile-quantile plots could be help:
For the ‘No Cancer’ group:
qqnorm(skinfold$Skinfold[which(skinfold$Group =='No Cancer')])
qqline(skinfold$Skinfold[which(skinfold$Group =='No Cancer')],lty=2)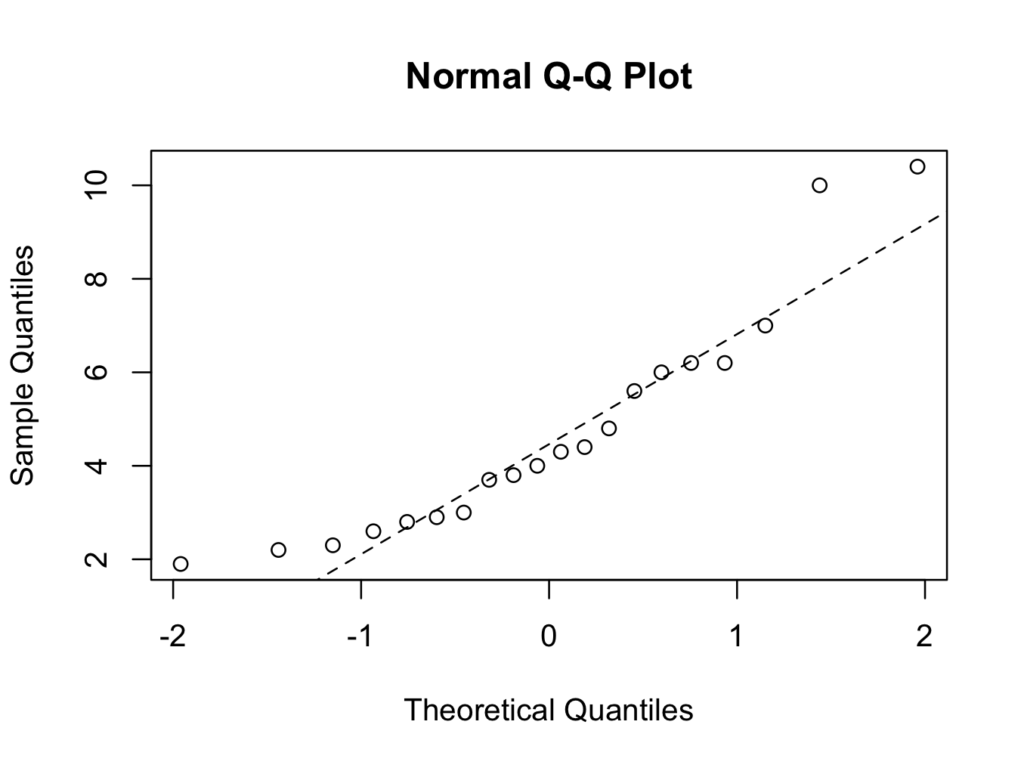
and for the ‘Cancer’ group:
qqnorm(skinfold$Skinfold[which(skinfold$Group =='Cancer')])
qqline(skinfold$Skinfold[which(skinfold$Group =='Cancer')],lty=2)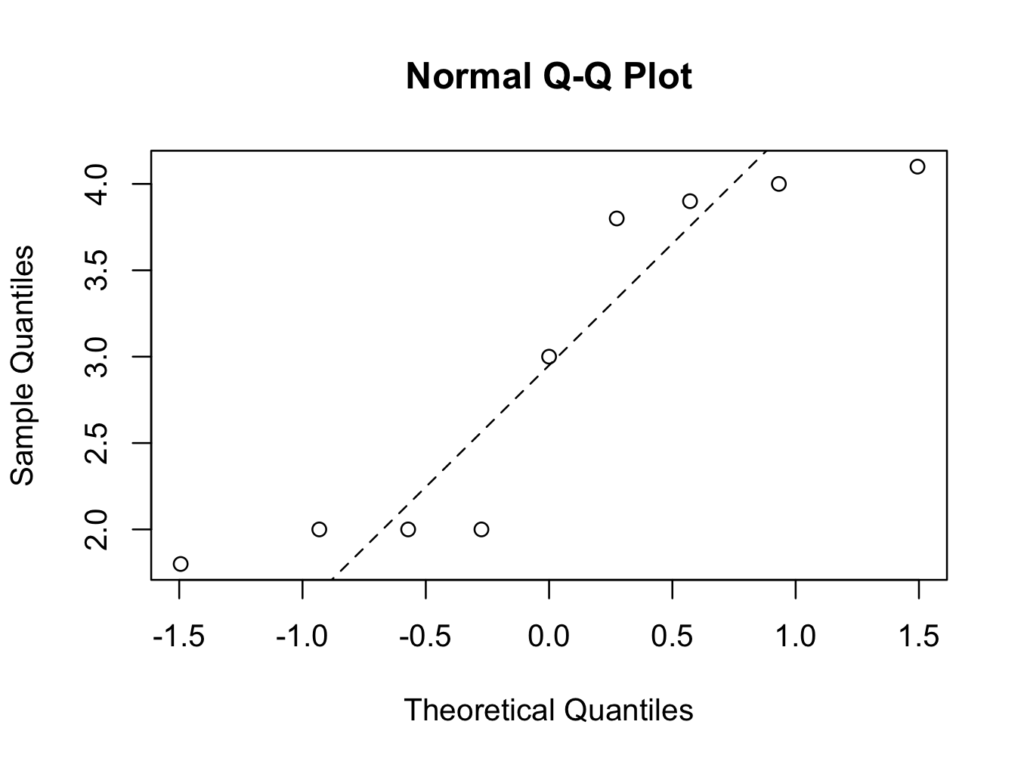
The number of patients in the ‘Cancer’ group is very small (9), but both groups fail the Normality tests. It is therefore more appropriate to use a non parametric test, in which it is not a requirement for data to conform a Normal distribution.