Introduction
Easter falls on the first Sunday after the first full moon following the beginning of the spring (vernal equinox) on the northern hemisphere.
The equinox is the moment when the plane of the earth’s equator passes through the centre of the sun; so when the centre of the sun is directly above the earth’s equator. This happens twice a year: around 21 March and the 21 September. On the day of the equinox, day and night are roughly of equal length (12 hours) everywhere on earth (even at the north pole and south pole).
The spring (vernal) equinox is a moment in time and it doesn’t fall on the same day each year. A table with the equinox times can be downloaded here and is shown below:
| March Equinox | June Solstice | September Equinox | December Solstice |
|---|---|---|---|
| 20/03/2000@07:35 GMT | 21/06/2000@02:47 BST | 22/09/2000@18:27 BST | 21/12/2000@13:37 GMT |
| 20/03/2001@13:30 GMT | 21/06/2001@08:37 BST | 23/09/2001@00:04 BST | 21/12/2001@19:21 GMT |
| 20/03/2002@19:16 GMT | 21/06/2002@14:24 BST | 23/09/2002@05:55 BST | 22/12/2002@01:14 GMT |
| 21/03/2003@00:59 GMT | 21/06/2003@20:10 BST | 23/09/2003@11:46 BST | 22/12/2003@07:03 GMT |
| 20/03/2004@06:48 GMT | 21/06/2004@01:56 BST | 22/09/2004@17:29 BST | 21/12/2004@12:41 GMT |
| 20/03/2005@12:33 GMT | 21/06/2005@07:46 BST | 22/09/2005@23:23 BST | 21/12/2005@18:34 GMT |
| 20/03/2006@18:25 GMT | 21/06/2006@13:25 BST | 23/09/2006@05:03 BST | 22/12/2006@00:22 GMT |
| 21/03/2007@00:07 GMT | 21/06/2007@19:06 BST | 23/09/2007@10:51 BST | 22/12/2007@06:07 GMT |
| 20/03/2008@05:48 GMT | 21/06/2008@00:59 BST | 22/09/2008@16:44 BST | 21/12/2008@12:03 GMT |
| 20/03/2009@11:43 GMT | 21/06/2009@06:45 BST | 22/09/2009@22:18 BST | 21/12/2009@17:46 GMT |
| 20/03/2010@17:32 GMT | 21/06/2010@12:28 BST | 23/09/2010@04:08 BST | 21/12/2010@23:38 GMT |
| 20/03/2011@23:20 GMT | 21/06/2011@18:16 BST | 23/09/2011@10:04 BST | 22/12/2011@05:30 GMT |
| 20/03/2012@05:14 GMT | 21/06/2012@00:08 BST | 22/09/2012@15:48 BST | 21/12/2012@11:11 GMT |
| 20/03/2013@11:01 GMT | 21/06/2013@06:03 BST | 22/09/2013@21:44 BST | 21/12/2013@17:11 GMT |
| 20/03/2014@16:57 GMT | 21/06/2014@11:51 BST | 23/09/2014@03:29 BST | 21/12/2014@23:03 GMT |
| 20/03/2015@22:45 GMT | 21/06/2015@17:37 BST | 23/09/2015@09:20 BST | 22/12/2015@04:47 GMT |
| 20/03/2016@04:30 GMT | 20/06/2016@23:34 BST | 22/09/2016@15:21 BST | 21/12/2016@10:44 GMT |
| 20/03/2017@10:28 GMT | 21/06/2017@05:24 BST | 22/09/2017@21:01 BST | 21/12/2017@16:27 GMT |
| 20/03/2018@16:15 GMT | 21/06/2018@11:07 BST | 23/09/2018@02:54 BST | 21/12/2018@22:22 GMT |
| 20/03/2019@21:58 GMT | 21/06/2019@16:54 BST | 23/09/2019@08:50 BST | 22/12/2019@04:19 GMT |
| 20/03/2020@03:49 GMT | 20/06/2020@22:43 BST | 22/09/2020@14:30 BST | 21/12/2020@10:02 GMT |
| 20/03/2021@09:37 GMT | 21/06/2021@04:32 BST | 22/09/2021@20:21 BST | 21/12/2021@15:59 GMT |
| 20/03/2022@15:33 GMT | 21/06/2022@10:13 BST | 23/09/2022@02:03 BST | 21/12/2022@21:48 GMT |
| 20/03/2023@21:24 GMT | 21/06/2023@15:57 BST | 23/09/2023@07:50 BST | 22/12/2023@03:27 GMT |
| 20/03/2024@03:06 GMT | 20/06/2024@21:50 BST | 22/09/2024@13:43 BST | 21/12/2024@09:20 GMT |
| 20/03/2025@09:01 GMT | 21/06/2025@03:42 BST | 22/09/2025@19:19 BST | 21/12/2025@15:03 GMT |
| 20/03/2026@14:45 GMT | 21/06/2026@09:24 BST | 23/09/2026@01:05 BST | 21/12/2026@20:50 GMT |
| 20/03/2027@20:24 GMT | 21/06/2027@15:10 BST | 23/09/2027@07:01 BST | 22/12/2027@02:42 GMT |
| 20/03/2028@02:17 GMT | 20/06/2028@21:01 BST | 22/09/2028@12:45 BST | 21/12/2028@08:19 GMT |
| 20/03/2029@08:02 GMT | 21/06/2029@02:48 BST | 22/09/2029@18:38 BST | 21/12/2029@14:14 GMT |
| 20/03/2030@13:51 GMT | 21/06/2030@08:31 BST | 23/09/2030@00:26 BST | 21/12/2030@20:09 GMT |
| 20/03/2031@19:41 GMT | 21/06/2031@14:17 BST | 23/09/2031@06:15 BST | 22/12/2031@01:55 GMT |
| 20/03/2032@01:21 GMT | 20/06/2032@20:08 BST | 22/09/2032@12:10 BST | 21/12/2032@07:55 GMT |
| 20/03/2033@07:22 GMT | 21/06/2033@02:01 BST | 22/09/2033@17:51 BST | 21/12/2033@13:45 GMT |
| 20/03/2034@13:17 GMT | 21/06/2034@07:44 BST | 22/09/2034@23:39 BST | 21/12/2034@19:33 GMT |
| 20/03/2035@19:02 GMT | 21/06/2035@13:33 BST | 23/09/2035@05:38 BST | 22/12/2035@01:30 GMT |
| 20/03/2036@01:02 GMT | 20/06/2036@19:32 BST | 22/09/2036@11:23 BST | 21/12/2036@07:12 GMT |
| 20/03/2037@06:50 GMT | 21/06/2037@01:22 BST | 22/09/2037@17:13 BST | 21/12/2037@13:07 GMT |
| 20/03/2038@12:40 GMT | 21/06/2038@07:09 BST | 22/09/2038@23:02 BST | 21/12/2038@19:02 GMT |
| 20/03/2039@18:31 GMT | 21/06/2039@12:57 BST | 23/09/2039@04:49 BST | 22/12/2039@00:40 GMT |
| 20/03/2040@00:11 GMT | 20/06/2040@18:46 BST | 22/09/2040@10:44 BST | 21/12/2040@06:32 GMT |
| 20/03/2041@06:06 GMT | 21/06/2041@00:35 BST | 22/09/2041@16:26 BST | 21/12/2041@12:18 GMT |
| 20/03/2042@11:53 GMT | 21/06/2042@06:15 BST | 22/09/2042@22:11 BST | 21/12/2042@18:04 GMT |
| 20/03/2043@17:27 GMT | 21/06/2043@11:58 BST | 23/09/2043@04:06 BST | 22/12/2043@00:01 GMT |
| 19/03/2044@23:20 GMT | 20/06/2044@17:51 BST | 22/09/2044@09:47 BST | 21/12/2044@05:43 GMT |
| 20/03/2045@05:07 GMT | 20/06/2045@23:33 BST | 22/09/2045@15:32 BST | 21/12/2045@11:35 GMT |
| 20/03/2046@10:57 GMT | 21/06/2046@05:14 BST | 22/09/2046@21:21 BST | 21/12/2046@17:28 GMT |
| 20/03/2047@16:52 GMT | 21/06/2047@11:03 BST | 23/09/2047@03:08 BST | 21/12/2047@23:07 GMT |
| 19/03/2048@22:33 GMT | 20/06/2048@16:53 BST | 22/09/2048@09:00 BST | 21/12/2048@05:02 GMT |
| 20/03/2049@04:28 GMT | 20/06/2049@22:47 BST | 22/09/2049@14:42 BST | 21/12/2049@10:52 GMT |
The date Easter can fall seems dependent on two cyclic events:
- Vernal Equinox
- Moon cycle
However, although the astronomical equinox falls on different days, the ecclesiastical date is fixed by convention on 21st March. Furthermore, the astronomical full moon is not exactly identical to the Paschal full moon as described in the ecclesiastical rules. Consequently, the earliest date Easter can fall is on the 22nd March and latest date is the 25th April.
Perhaps it is expected that, in the long term, the date Easter falls has a uniform distribution. In other words; the proportion of Easters falling on a particular date is the same as on any other possible date (between 22nd March and 25th April). But is the distribution uniform?
This paper has two sections. In the first section, the distribution of the date Easter falls is examined using the timeDate1 package. Subsequently, the dates are compared with dates calculated using the phases of the moon using the lunar2 package.
Install Packages
The following packages should be installed as described:
- dplyR package3, to manipulate data frames
- ggplot2 package4, to create plots
- lubridate package5, to work with dates
- timeDate package6, to extract Easter dates
- lunar package7, another package to calculate full moon
Distribution of Easter Dates
100 Years from 2000
To find the dates of Easter from 2000 onwards is straight forward with the timeDate8 package. Load the necessary libraries and create a vector (Easter_100) with 100 Easter dates from 2000 onwards:
library(timeDate)
library(dplyr)
library(ggplot2)
Easter_100 <- Easter(2000:2100) # Easter dates from 2000Extract the year, month and day from the date and convert to a data frame called Easter_100_dates:
Easter_100_year <- as.numeric(strftime(Easter_100, format = '%Y'))
Easter_100_month <- as.numeric(strftime(Easter_100, format = '%m'))
Easter_100_day <- as.numeric(strftime(Easter_100, format = '%d'))
Easter_100_dates <- data.frame(Easter_100_year, Easter_100_month, Easter_100_day)To show the data frame:
Easter_100_dates
Easter_100_year Easter_100_month Easter_100_day
1 2000 4 23
- - - -
101 2100 3 28Summarise the data with dplyR9:
#summarise the data and calculate frequencies:
Easter_100_summary <- Easter_100_dates %>%
dplyr::group_by(Easter_100_month, Easter_100_day) %>%
dplyr::tally() # function in dplyr to add up groupsAdd the percentage each day is Easter Sunday and show the data:
Easter_100_summary$perc = 100 * Easter_100_summary$n / sum(Easter_100_summary$n)
Easter_100_summary
# A tibble: 33 x 4
# Groups: Easter_100_month [?]
Easter_100_month Easter_100_day n perc
<dbl> <dbl> <int> <dbl>
1 3. 23. 1 0.990
2 3. 25. 2 1.98
3 3. 26. 3 2.97
4 3. 27. 2 1.98
5 3. 28. 3 2.97
6 3. 29. 3 2.97
7 3. 30. 4 3.96
8 3. 31. 5 4.95
9 4. 1. 3 2.97
10 4. 2. 2 1.98
# ... with 23 more rowsCreate a vector for the x axis, to make the plot that follows more readable:
# Create a vector for the x-axis labels, to make the axis more readable:
axis_label <- c('22.3' = '22', '23.3' = '23', '24.3' = '24', '25.3' = '25', '26.3' = '26', '27.3' = '27', '28.3' = '28', '29.3' = '29', '30.3' = '30', '31.3' = '31', '1.4' = '1', '2.4' = '2', '3.4' = '3', '4.4' = '4', '5.4' = '5', '6.4' = '6', '7.4' = '7', '8.4' = '8', '9.4' = '9', '10.4' = '10', '11.4' = '11', '12.4' = '12', '13.4' = '13', '14.4' = '14', '15.4' = '15', '16.4' = '16', '17.4' = '17', '18.4' = '18', '19.4' = '19', '20.4' = '20', '21.4' = '21', '22.4' = '22', '23.4' = '23', '24.4' = '24', '25.4' = '25' )And create a plot with ggplot210:
plot_100 <- Easter_100_summary %>%
ggplot() +
geom_bar(aes(x = interaction(Easter_100_day, Easter_100_month), y = perc ), stat = 'identity', colour = 'black', fill = 'blue') +
ylab('Proportion of Easter Sunday on day [%]') +
ggtitle(label = 'Easter between 2000 and 2100') +
scale_x_discrete('Date', labels = axis_label) +
geom_text(label = 'March', x = 4, y = -0.1) +
geom_text(label = 'April', x = 10, y = -0.1) +
theme_bw()
dev.new()
plot_100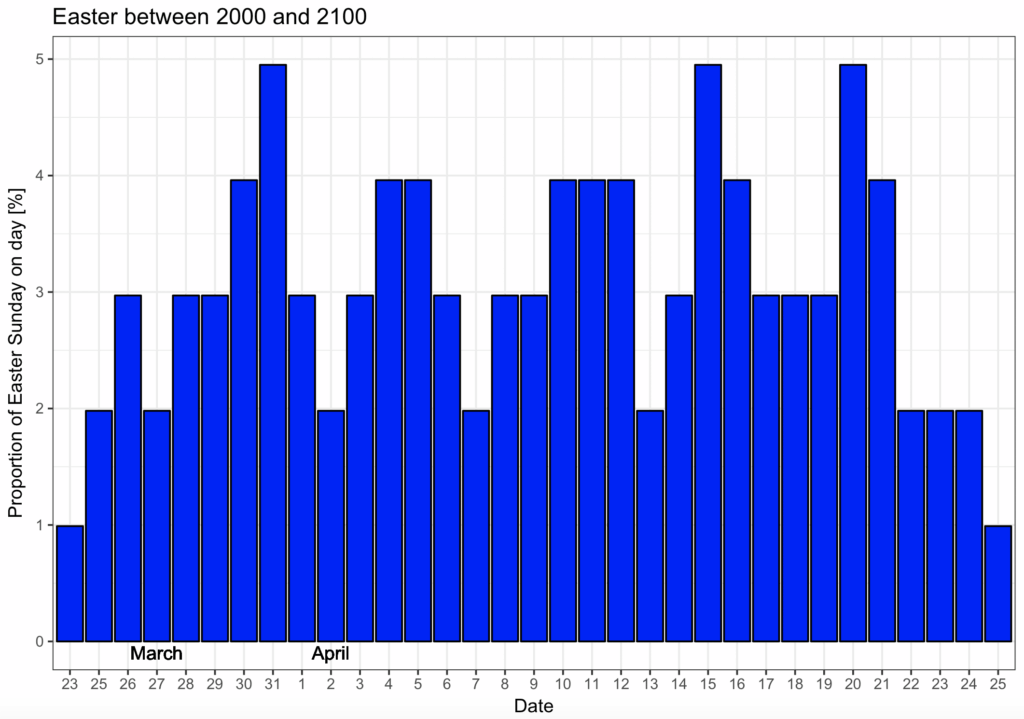
The plot clearly shows that the distribution of Easter dates is not uniform. The increase in proportion of Easters between 23rd March and 26th March as well as the decrease in proportion of Easters between 22nd April and 25th April are appreciated as they are at the beginning and end of the plot. However, the 31st March, 15th April and 20 April are more common Easter dates than other dates and 27th March, 2nd April, 7th April and 13th April are less common dates for Easter.
1000 Years from beginning Gregorian Calendar
Perhaps the unexpected distribution in dates is due to a relatively small number of dates? Similarly, it is easy to look from the beginning of the Gregorian calendar (1583) to the year 3000:
# Easter from beginning Gregorian calendar to year 3000
Easter_3000 <- Easter(1583:3000)
Easter_3000_year <- as.numeric(strftime(Easter_3000, format = '%Y'))
Easter_3000_month <- as.numeric(strftime(Easter_3000, format = '%m'))
Easter_3000_day <- as.numeric(strftime(Easter_3000, format = '%d'))
Easter_3000_dates <- data.frame(Easter_3000_year, Easter_3000_month, Easter_3000_day)
#summarise the data and calculate frequencies:
Easter_3000_summary <- Easter_3000_dates %>%
dplyr::group_by(Easter_3000_month, Easter_3000_day) %>%
dplyr::tally() # function in dplyr to add up groups
Easter_3000_summary$perc = 100 * Easter_3000_summary$n / sum(Easter_3000_summary$n) # calculate percentage
plot_3000 <- Easter_3000_summary %>%
ggplot() +
geom_bar(aes(x = interaction(Easter_3000_day, Easter_3000_month), y = perc), stat = 'identity', colour = 'black', fill = 'red') +
ylab('Proportion of Easter Sunday on day [%]') +
ggtitle(label = 'Easter between 1583 and 3000') +
scale_x_discrete('Date', labels = axis_label) +
geom_text(label = 'March', x = 4, y = -0.1) +
geom_text(label = 'April', x = 12, y = -0.1) +
theme_bw()
dev.new()
plot_3000
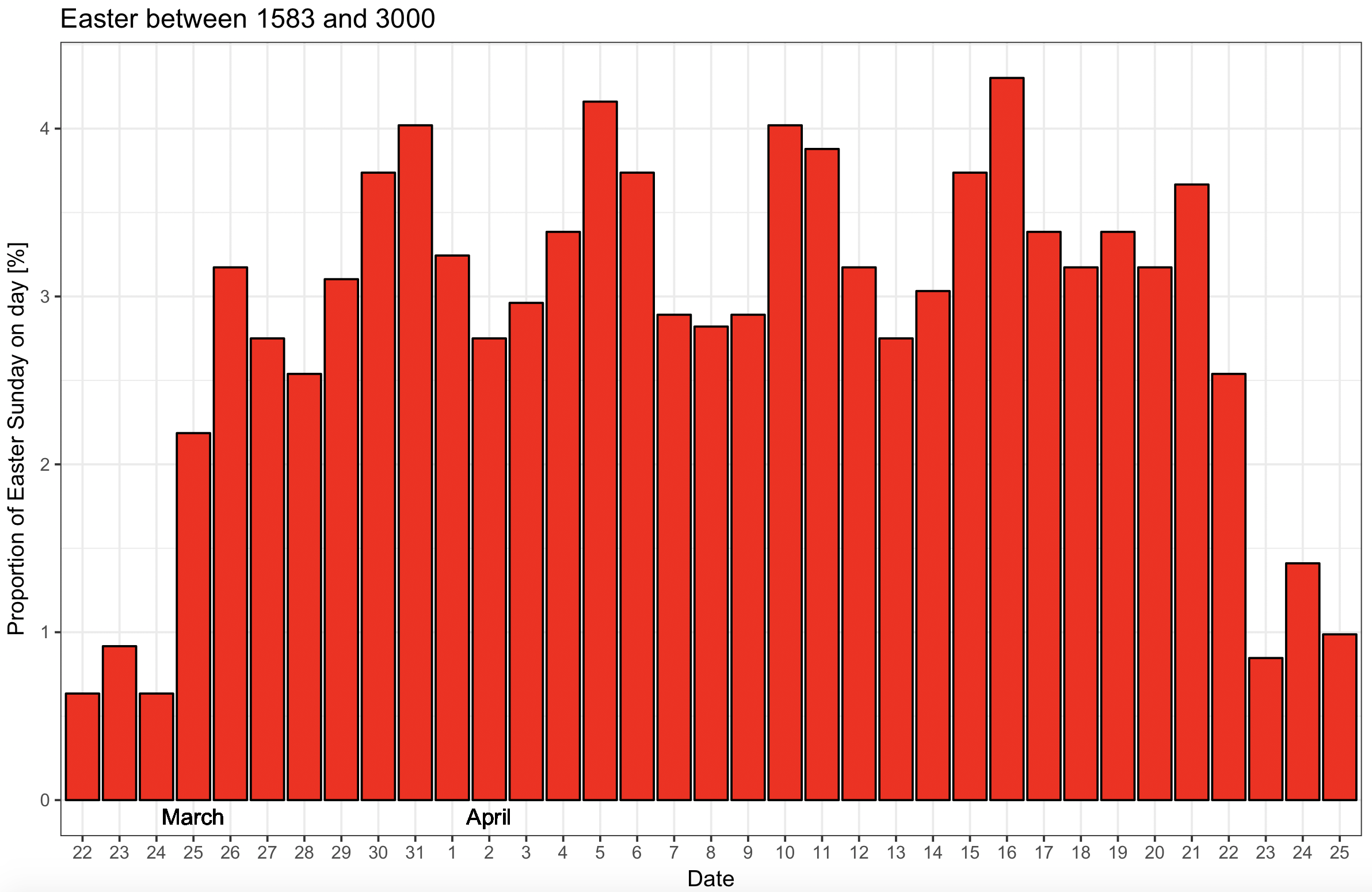
Still not a uniform distribution! Again, there are dips in the distribution, similarly to the previous plot. Perhaps we should look at even more dates?
10,000 Years from beginning Gregorian Calendar
Similarly, look at 10,000 years; from the beginning of the Gregorian calendar to the year 10,000:
# Easter from the beginning of the Gregorian calendar to the year 9999
Easter_10k <- Easter(1583:9999)
Easter_10k_year <- as.numeric(strftime(Easter_10k, format = '%Y'))
Easter_10k_month <- as.numeric(strftime(Easter_10k, format = '%m'))
Easter_10k_day <- as.numeric(strftime(Easter_10k, format = '%d'))
Easter_10k_dates <- data.frame(Easter_10k_year, Easter_10k_month, Easter_10k_day)
#summarise the data and calculate frequencies:
Easter_10k_summary <- Easter_10k_dates %>%
dplyr::group_by(Easter_10k_month, Easter_10k_day) %>%
dplyr::tally() # function in dplyr to add up groups
Easter_10k_summary$perc <- 100 * Easter_10k_summary$n / sum(Easter_10k_summary$n) # calculate percentage
plot_10k <- Easter_10k_summary %>%
ggplot() +
geom_bar(aes(x = interaction(Easter_10k_day, Easter_10k_month), y = perc), stat = 'identity', colour = 'black', fill = 'green') +
ylab('Proportion of Easter Sunday on day [%]') +
ggtitle(label = 'Easter between 1583 and 9999') +
scale_x_discrete('Date', labels = axis_label) +
geom_text(label = 'March', x = 4, y = -0.1) +
geom_text(label = 'April', x = 12, y = -0.1) +
theme_bw()
dev.new()
plot_10k 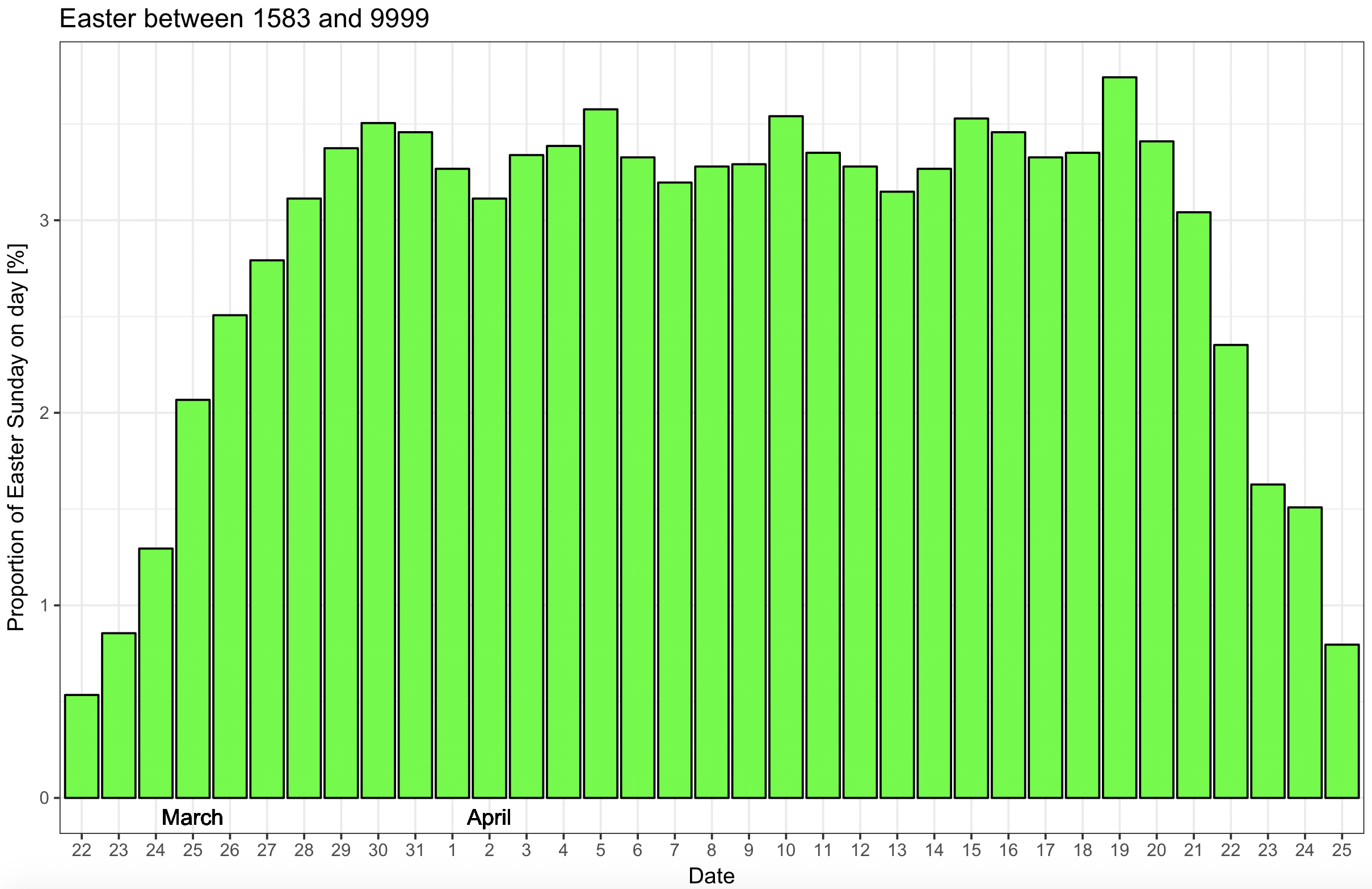
Perhaps the distribution is just not uniform? Although better, there are still cyclic dips in the plot and 19th April is the most common date for Easter Sunday.
Conclusion
The distribution of the Easter dates is not uniform and 19th April is the most common Easter date.
Phases of the Moon
Above, the Easter dates were extracted from the timeDate package11. Next, this Easter date is compared to the date calculated with the lunar package12.
First load the packages:
library(dplyr)
library(ggplot2)
library(lubridate)
library(timeDate)
library(lunar)The moon completes its orbit around the earth every 27.3 days (sidereal month). However, due to the motion of the earth around the sun, it takes longer for the moon to take the same relative position to earth (synodic month). A synodic month is on average 29.5 days, but subject to variation due to complex orbital effects.
First create a vector with possible dates for a full moon on or after 21st March for the next 101 years. The loop below runs 101 times (from 0 to 100) and should create a vector of 3030 dates:
dates <- NULL # create a null vector to append dates to.
for (n in 0:100){
start <- as.Date("2000-03-21") + years(n)
date <- seq(start, by = "day", length.out = 30)
dates <- append(dates, date)
}Examine the length (should be 3030), head and tail of the vector:
length(dates)
[1] 3030
# show the head and tail of the vector
head(dates)
[1] "2000-03-21" "2000-03-22" "2000-03-23" "2000-03-24" "2000-03-25" "2000-03-26"
tail(dates)
[1] "2100-04-14" "2100-04-15" "2100-04-16" "2100-04-17" "2100-04-18" "2100-04-19"Convert the dates vector to a data frame (called Easters) and add the date of Easter (as calculated with the Easter function in the timeDate13 package) to the data frame. The Easter function returns a timeDate object that should be converted to a date for subsequent manipulation:
# convert the dates vector to a data frame called Easters:
Easters <- data.frame("Date" = dates)
# find the date Easter falls within that year
# should be the same for all 30 days within a given year
Easters$Easter <- Easter(year(Easters$Date))
# the Easter date is returned as a dateTime object; convert to a date:
Easters$Easter <- as.Date(Easters$Easter)Extract the year, month, day, week-day name and week-day number from the date. This is required to calculate the Julian date:
Easters$Year <- year(Easters$Date)
Easters$Month <- month(Easters$Date)
Easters$Day <- day(Easters$Date)
Easters$Week_day <- weekdays(Easters$Date)
Easters$Week_day_number <- as.numeric(format(Easters$Date, "%w"))Week-day numbers are counted from Sunday; with Sunday = 0 and Monday = 1.
What would the day of Easter be if the date was a full moon? Easter would be the next Sunday and Sunday a week later if the full moon is on a Sunday.
# if on a Sunday, a week later, otherwise the next Sunday:
Easters$Easter_calc <- Easters$Date + days(7 - Easters$Week_day_number)By convention, Easter can’t fall on the 21st March. Consequently if full moon is on the 21st March, Easter will be four weeks (28 days) later:
Easters$Easter_calc <- if_else(Easters$Month == 3 & Easters$Day == 21, Easters$Easter_calc + 28, Easters$Easter_calc)What would the difference between the calculated and actual Easter date be?
Easters$Easter_diff <- Easters$Easter - Easters$Easter_calc
summary(Easters$Easter_diff)
Time differences in days
Min. 1st Qu. Median Mean 3rd Qu. Max.
-28.0000 -7.0000 0.0000 -0.3142 7.0000 28.0000 Examine the data frame:
str(Easters)
'data.frame': 3030 obs. of 9 variables:
$ Date : Date, format: "2000-03-21" "2000-03-22" "2000-03-23" "2000-03-24" ...
$ Easter : Date, format: "2000-04-23" "2000-04-23" "2000-04-23" "2000-04-23" ...
$ Year : num 2000 2000 2000 2000 2000 2000 2000 2000 2000 2000 ...
$ Month : num 3 3 3 3 3 3 3 3 3 3 ...
$ Day : int 21 22 23 24 25 26 27 28 29 30 ...
$ Week_day : chr "Tuesday" "Wednesday" "Thursday" "Friday" ...
$ Week_day_number: num 2 3 4 5 6 0 1 2 3 4 ...
$ Easter_calc : Date, format: "2000-04-23" "2000-03-26" "2000-03-26" "2000-03-26" ...
$ Easter_diff : 'difftime' num 0 28 28 28 ...
..- attr(*, "control")= Named chr [1:2] "trunc" "GMT"
.. ..- attr(*, "names")= chr [1:2] "method" "FinCenter"
..- attr(*, "units")= chr "days"
head(Easters)
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff
1 2000-03-21 2000-04-23 2000 3 21 Tuesday 2 2000-04-23 0 days
2 2000-03-22 2000-04-23 2000 3 22 Wednesday 3 2000-03-26 28 days
3 2000-03-23 2000-04-23 2000 3 23 Thursday 4 2000-03-26 28 days
4 2000-03-24 2000-04-23 2000 3 24 Friday 5 2000-03-26 28 days
5 2000-03-25 2000-04-23 2000 3 25 Saturday 6 2000-03-26 28 days
6 2000-03-26 2000-04-23 2000 3 26 Sunday 0 2000-04-02 21 days
tail(Easters)
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff
3025 2100-04-14 2100-03-28 2100 4 14 Wednesday 3 2100-04-18 -21 days
3026 2100-04-15 2100-03-28 2100 4 15 Thursday 4 2100-04-18 -21 days
3027 2100-04-16 2100-03-28 2100 4 16 Friday 5 2100-04-18 -21 days
3028 2100-04-17 2100-03-28 2100 4 17 Saturday 6 2100-04-18 -21 days
3029 2100-04-18 2100-03-28 2100 4 18 Sunday 0 2100-04-25 -28 days
3030 2100-04-19 2100-03-28 2100 4 19 Monday 1 2100-04-25 -28 days
When is full moon? This can be calculated with the lunar package14. The illumination of the moon can be shifted to midnight (12 hours) to calculate the lunar illumination at the beginning of the day.
# calculate the illumination of the moon, shifted to midnight (by 12 hours)
Easters$Phase_lunar <- lunar.illumination(Easters$Date, shift = -12)Find the full moons as calculated by the lunar15 package and save the result in a new data frame called full_moons_lunar:
full_moons_lunar <- Easters %>%
dplyr::group_by(Year) %>%
dplyr::filter(Phase_lunar == max(Phase_lunar))Have a look at the data frame:
head(full_moons_lunar)
# A tibble: 6 × 10
# Groups: Year [6]
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff Phase_lunar
<date> <date> <dbl> <dbl> <int> <chr> <dbl> <date> <drtn> <dbl>
1 2000-04-19 2000-04-23 2000 4 19 Wednesday 3 2000-04-23 0 days 1.00
2 2001-04-08 2001-04-15 2001 4 8 Sunday 0 2001-04-15 0 days 0.999
3 2002-03-29 2002-03-31 2002 3 29 Friday 5 2002-03-31 0 days 0.999
4 2003-04-17 2003-04-20 2003 4 17 Thursday 4 2003-04-20 0 days 0.998
5 2004-04-05 2004-04-11 2004 4 5 Monday 1 2004-04-11 0 days 1.00
6 2005-03-25 2005-03-27 2005 3 25 Friday 5 2005-03-27 0 days 0.999
tail(full_moons_lunar)
# A tibble: 6 × 10
# Groups: Year [6]
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff Phase_lunar
<date> <date> <dbl> <dbl> <int> <chr> <dbl> <date> <drtn> <dbl>
1 2095-03-21 2095-04-24 2095 3 21 Monday 1 2095-04-24 0 days 1.00
2 2096-04-08 2096-04-15 2096 4 8 Sunday 0 2096-04-15 0 days 0.999
3 2097-03-28 2097-03-31 2097 3 28 Thursday 4 2097-03-31 0 days 1.00
4 2098-04-16 2098-04-20 2098 4 16 Wednesday 3 2098-04-20 0 days 1.00
5 2099-04-05 2099-04-12 2099 4 5 Sunday 0 2099-04-12 0 days 0.998
6 2100-03-26 2100-03-28 2100 3 26 Friday 5 2100-03-28 0 days 0.999
length(full_moons_lunar)
[1] 10
nrow(full_moons_lunar)
[1] 101Select the were the difference between calculated Easter date and actual Easter date is not null (!=0):
# select the rows where the difference is not null
full_moons_lunar[full_moons_lunar$Easter_diff != 0, ]
# A tibble: 2 × 10
# Groups: Year [2]
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff Phase_lunar
<date> <date> <dbl> <dbl> <int> <chr> <dbl> <date> <drtn> <dbl>
1 2018-04-01 2018-04-01 2018 4 1 Sunday 0 2018-04-08 -7 days 0.999
2 2076-04-19 2076-04-19 2076 4 19 Sunday 0 2076-04-26 -7 days 0.999The calculated day was wrong only twice; on both occasions when full moon was on a Sunday. How many times full moon was on a Sunday?
# select the rows where the full moon is on a sunday
full_moons_lunar[full_moons_lunar$Week_day == "Sunday",]
# A tibble: 16 × 10
# Groups: Year [16]
Date Easter Year Month Day Week_day Week_day_number Easter_calc Easter_diff Phase_lunar
<date> <date> <dbl> <dbl> <int> <chr> <dbl> <date> <drtn> <dbl>
1 2001-04-08 2001-04-15 2001 4 8 Sunday 0 2001-04-15 0 days 0.999
2 2018-04-01 2018-04-01 2018 4 1 Sunday 0 2018-04-08 -7 days 0.999
3 2021-03-28 2021-04-04 2021 3 28 Sunday 0 2021-04-04 0 days 0.998
4 2025-04-13 2025-04-20 2025 4 13 Sunday 0 2025-04-20 0 days 1.00
5 2038-03-21 2038-04-25 2038 3 21 Sunday 0 2038-04-25 0 days 1.00
6 2045-04-02 2045-04-09 2045 4 2 Sunday 0 2045-04-09 0 days 1.00
7 2052-04-14 2052-04-21 2052 4 14 Sunday 0 2052-04-21 0 days 1.00
8 2065-03-22 2065-03-29 2065 3 22 Sunday 0 2065-03-29 0 days 1.00
9 2069-04-07 2069-04-14 2069 4 7 Sunday 0 2069-04-14 0 days 0.998
10 2072-04-03 2072-04-10 2072 4 3 Sunday 0 2072-04-10 0 days 1.00
11 2076-04-19 2076-04-19 2076 4 19 Sunday 0 2076-04-26 -7 days 0.999
12 2079-04-16 2079-04-23 2079 4 16 Sunday 0 2079-04-23 0 days 0.999
13 2089-03-27 2089-04-03 2089 3 27 Sunday 0 2089-04-03 0 days 0.998
14 2092-03-23 2092-03-30 2092 3 23 Sunday 0 2092-03-30 0 days 0.999
15 2096-04-08 2096-04-15 2096 4 8 Sunday 0 2096-04-15 0 days 0.999
16 2099-04-05 2099-04-12 2099 4 5 Sunday 0 2099-04-12 0 days 0.998So the calculated Easter date was wrong two out of 16 times (01/04/2018 and 19/04/2076; 13%). Both dates were when full moon was on a Sunday. Presumably this is related to the exact timing of full moon? Let’s have a look at that by making a vector and find the exact timing of full moon on both dates. First for 2018:
# first create a vector of 24 hours:
hours <- seq(1, by = 1, length.out = 24)
# create a shift vector from -24 to 0)
shift <- seq(-24, by = 1, length.out = 24 )
# convert to a data frame
hours <- data.frame("hours" = hours, "shift" = shift)
# add the date:
hours$date <- as.Date("2018-04-01")
# calculate lunar illumunation with the lunar package and add to data frame
hours$illumination <- lunar.illumination(hours$date, shift = hours$shift)
hours
hours shift date illumination
1 1 -24 2018-04-01 0.9993053
2 2 -23 2018-04-01 0.9995192
3 3 -22 2018-04-01 0.9996939
4 4 -21 2018-04-01 0.9998294
5 5 -20 2018-04-01 0.9999255
6 6 -19 2018-04-01 0.9999824
7 7 -18 2018-04-01 0.9999999
8 8 -17 2018-04-01 0.9999782
9 9 -16 2018-04-01 0.9999172
10 10 -15 2018-04-01 0.9998169
11 11 -14 2018-04-01 0.9996772
12 12 -13 2018-04-01 0.9994984
13 13 -12 2018-04-01 0.9992802
14 14 -11 2018-04-01 0.9990229
15 15 -10 2018-04-01 0.9987263
16 16 -9 2018-04-01 0.9983905
17 17 -8 2018-04-01 0.9980155
18 18 -7 2018-04-01 0.9976014
19 19 -6 2018-04-01 0.9971482
20 20 -5 2018-04-01 0.9966559
21 21 -4 2018-04-01 0.9961246
22 22 -3 2018-04-01 0.9955543
23 23 -2 2018-04-01 0.9949450
24 24 -1 2018-04-01 0.9942969
# find the max value:
full_moon_2018 <- hours[hours$illumination == max(hours$illumination),]
full_moon_2018
hours shift date illumination
7 7 -18 2018-04-01 0.9999999So a shift of 18 hours confirms that full moon was actually on a Saturday and not a Sunday. Similarly for 2076:
hours <- seq(1, by = 1, length.out = 24)
# create a shift vector from -24 to 0)
shift <- seq(-24, by = 1, length.out = 24 )
# convert to a data frame
hours <- data.frame("hours" = hours, "shift" = shift)
# add the date:
hours$date <- as.Date("2076-04-19")
# calculate lunar illumunation with the lunar package and add to data frame
hours$illumination <- lunar.illumination(hours$date, shift = hours$shift)
hours
hours shift date illumination
1 1 -24 2076-04-19 0.9994982
2 2 -23 2076-04-19 0.9996771
3 3 -22 2076-04-19 0.9998168
4 4 -21 2076-04-19 0.9999171
5 5 -20 2076-04-19 0.9999782
6 6 -19 2076-04-19 0.9999999
7 7 -18 2076-04-19 0.9999824
8 8 -17 2076-04-19 0.9999256
9 9 -16 2076-04-19 0.9998295
10 10 -15 2076-04-19 0.9996941
11 11 -14 2076-04-19 0.9995194
12 12 -13 2076-04-19 0.9993055
13 13 -12 2076-04-19 0.9990523
14 14 -11 2076-04-19 0.9987599
15 15 -10 2076-04-19 0.9984283
16 16 -9 2076-04-19 0.9980576
17 17 -8 2076-04-19 0.9976476
18 18 -7 2076-04-19 0.9971986
19 19 -6 2076-04-19 0.9967105
20 20 -5 2076-04-19 0.9961834
21 21 -4 2076-04-19 0.9956172
22 22 -3 2076-04-19 0.9950121
23 23 -2 2076-04-19 0.9943681
24 24 -1 2076-04-19 0.9936853
# find the max value:
full_moon_2076 <- hours[hours$illumination == max(hours$illumination),]
full_moon_2076
hours shift date illumination
6 6 -19 2076-04-19 0.9999999So again, a shift of 19 hours indicates that the precise timing of full moon was actually on a Saturday, explaining the difference in calculated and actual date for Easter.
Conclusion
Overall, the lunar16 package allows to estimate the exact timing of full moon and subsequently deduct the date of Easter.
Errors in calculation of the Easter date can occur when full moon is late Saturday evening / night (just before Sunday). If not appreciated, this could result in the calculated date of Easter being a week later. It is possible to improve the estimation by calculating the exact timing of full moon when full moon falls on Sunday. Looking at the estimates from the lunar package:
full_moons_lunar[full_moons_lunar$Week_day == "Sunday", c("Date", "Easter", "Easter_calc", "Easter_diff", "Phase_lunar")]
# A tibble: 16 x 5
Date Easter Easter_calc Easter_diff Phase_lunar
<date> <date> <date> <time> <dbl>
1 2001-04-08 2001-04-15 2001-04-15 0 0.999
2 2018-04-01 2018-04-01 2018-04-08 -7 0.999
3 2021-03-28 2021-04-04 2021-04-04 0 0.998
4 2025-04-13 2025-04-20 2025-04-20 0 1.000
5 2038-03-21 2038-04-25 2038-04-25 0 1.000
6 2045-04-02 2045-04-09 2045-04-09 0 1.000
7 2052-04-14 2052-04-21 2052-04-21 0 1.000
8 2065-03-22 2065-03-29 2065-03-29 0 1.000
9 2069-04-07 2069-04-14 2069-04-14 0 0.998
10 2072-04-03 2072-04-10 2072-04-10 0 1.000
11 2076-04-19 2076-04-19 2076-04-26 -7 0.999
12 2079-04-16 2079-04-23 2079-04-23 0 0.999
13 2089-03-27 2089-04-03 2089-04-03 0 0.998
14 2092-03-23 2092-03-30 2092-03-30 0 0.999
15 2096-04-08 2096-04-15 2096-04-15 0 0.999
16 2099-04-05 2099-04-12 2099-04-12 0 0.998On both dates, lunar illumination was 99.9% but just after full moon. Four other estimates were lunar illumination was 99.9% and four were lunar illumination was 99.8% however were correct. All six estimates were lunar illumination was 100% were correct.
Overall, 100% accuracy can be obtained in calculating the date of Easter Sunday. If full moon is on a Sunday and illumination is less than 100%, the exact timing of full moon should be established to allow accurate prediction.