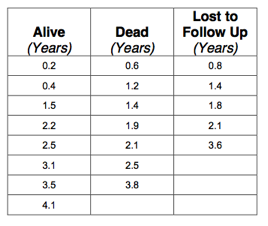
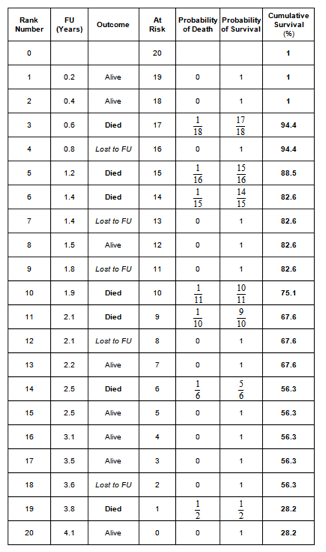
The table below shows 20 patients who have been diagnosed with cancer. The first column shows the follow up (in years) of the patients who were alive at review. In the second column, the follow up till time of death is indicated. The third column shows the time to last review in the patients who were lost to follow up:
The data is also available in Q9.rda and for convenience the table is shown below:
1. Calculate the 5-year survival in the best-case scenario, using life table analysis.
The best-case scenario is as follows:
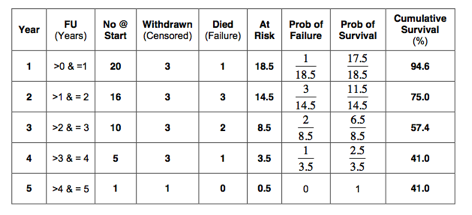
So, the 5-year survival in the best-case scenario as estimated with life table analysis is 41%.
2. Calculate the 5-year survival in the worst-case scenario, using life table analysis.
The worst-case scenario life table is as follows:
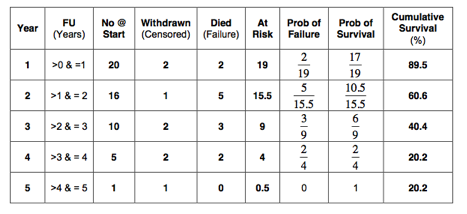
So, the 5-year survival in the worst-case scenario as estimated with life table analysis is 20%.
3. Show the best-case scenario and worst-case scenario survival curves in one graph, using life table analysis.
Using the tables constructed in Q1 and Q2, survival curves can be drawn:
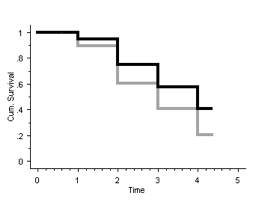
The best-case scenario is shown in black and the worst-case scenario is shown in grey.
4. Perform the Kaplan-Meier survival analysis in the best-case scenario.
In the best-case scenario, the patients lost to follow up count as a success. The Kaplan-Meier table is as follows:
In R:
Once the data frame is loaded, the data should be visible with the variables ‘Number’, ‘FU’ and ‘Outcome’.
load("/path/to_file/Q9 (1).rda")
Q9
Number FU Outcome
1 1 0.2 alive
2 2 0.4 alive
3 3 1.5 alive
4 4 2.2 alive
5 5 2.5 alive
6 6 3.1 alive
7 7 3.5 alive
8 8 4.1 alive
9 9 0.6 dead
10 10 1.2 dead
11 11 1.4 dead
12 12 1.9 dead
13 13 2.1 dead
14 14 2.5 dead
15 15 3.8 dead
16 16 0.8 lost
17 17 1.4 lost
18 18 1.8 lost
19 19 2.1 lost
20 20 3.6 lostIt is of course possible to create a new logical variable that is needed for survival analysis (called ‘Best’) and go through the data manually; setting the value to FALSE (0) if the ‘Outcome’ variable is ‘alive’ or ‘lost’ and TRUE (1) if the ‘Outcome’ variable is ‘dead’. However, this would become tedious for larger data sets. It would be easier to recode the variable ‘Outcome’ in a new variable ‘Best’.
Q9$Best <- ifelse(Q9$Outcome == 'dead', 1, 0)
Q9
Number FU Outcome Best
1 1 0.2 alive 0
2 2 0.4 alive 0
3 3 1.5 alive 0
4 4 2.2 alive 0
5 5 2.5 alive 0
6 6 3.1 alive 0
7 7 3.5 alive 0
8 8 4.1 alive 0
9 9 0.6 dead 1
10 10 1.2 dead 1
11 11 1.4 dead 1
12 12 1.9 dead 1
13 13 2.1 dead 1
14 14 2.5 dead 1
15 15 3.8 dead 1
16 16 0.8 lost 0
17 17 1.4 lost 0
18 18 1.8 lost 0
19 19 2.1 lost 0
20 20 3.6 lost 0
str(Q9)
'data.frame': 20 obs. of 4 variables:
$ Number : num 1 2 3 4 5 6 7 8 9 10 ...
$ FU : num 0.2 0.4 1.5 2.2 2.5 3.1 3.5 4.1 0.6 1.2 ...
$ Outcome: Factor w/ 3 levels "alive","dead",..: 1 1 1 1 1 1 1 1 2 2 ...
$ Best : num 0 0 0 0 0 0 0 0 1 1 ...If the variable Outcome (Q9$Outcome) is equal to (==) ‘dead’, then the Best variable (Q9$Best) = 1, else it is 0.
As can be seen in the structure of the data frame (str), the newly created variable ‘Best’ is numerical and takes values 0 and 1.
Now perform the survival analysis with the survival package1. Make sure the package survival is installed.
my_survival <- Surv(Q9$FU, Q9$Best)
my_survival
[1] 0.2+ 0.4+ 1.5+ 2.2+ 2.5+ 3.1+ 3.5+ 4.1+ 0.6 1.2 1.4 1.9 2.1 2.5 3.8 0.8+ 1.4+ 1.8+
[19] 2.1+ 3.6+
summary(my_survival)
time status
Min. :0.200 Min. :0.00
1st Qu.:1.350 1st Qu.:0.00
Median :2.000 Median :0.00
Mean :2.035 Mean :0.35
3rd Qu.:2.650 3rd Qu.:1.00
Max. :4.100 Max. :1.00 And calculate the survival curve:
my_curve <- survfit(my_survival ~ 1, conf.int = 0.95, data=Q9)
summary(my_curve)
Call: survfit(formula = my_survival ~ 1, data = Q9, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0.6 18 1 0.944 0.0540 0.8443 1.000
1.2 16 1 0.885 0.0763 0.7477 1.000
1.4 15 1 0.826 0.0913 0.6655 1.000
1.9 11 1 0.751 0.1096 0.5644 1.000
2.1 10 1 0.676 0.1217 0.4751 0.962
2.5 7 1 0.580 0.1374 0.3642 0.922
3.8 2 1 0.290 0.2161 0.0672 1.000Plot the curve:
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(my_curve, col='black', main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')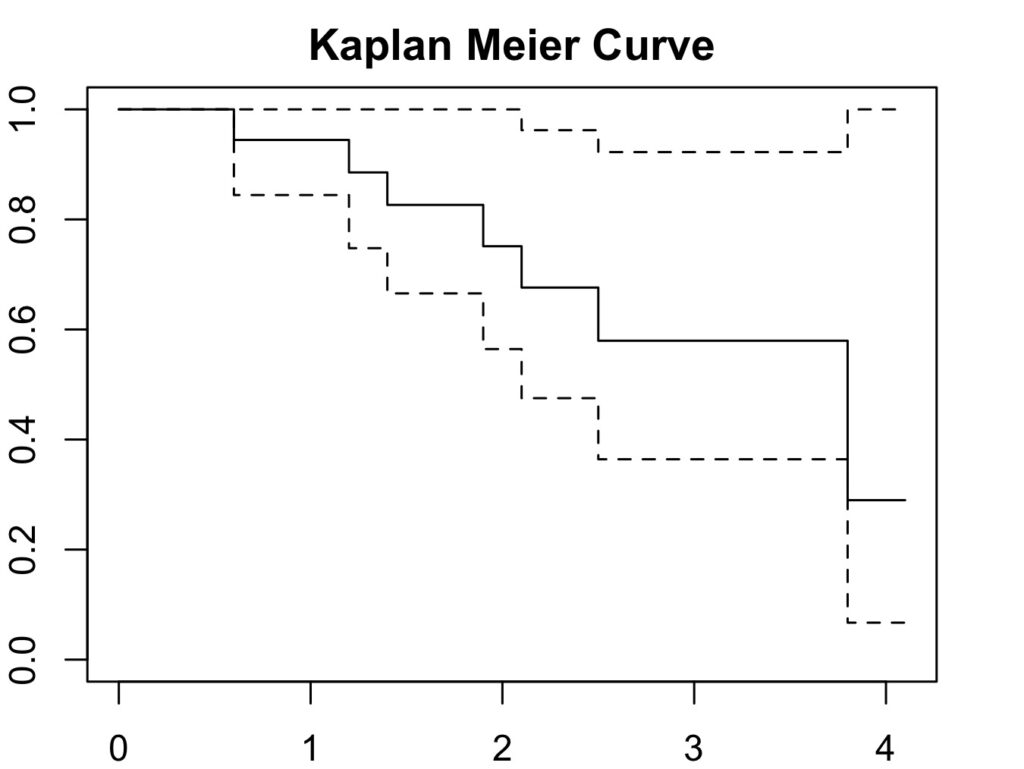
Please note the survival estimate is similar to the table above, but the last two values are slightly different due to rounding error.
5. What is the survival in Q4 at 4.1 years?
The survival at 4.1 years in the best-case scenario as estimated with Kaplan-Meier analysis as calculated in the table in Q4 above is 28%.
In R:
Using the output from R in Q4 above: 29%.
Or alternatively in the console on the recoded variable ‘Best’ following on from above:
summary(my_curve,time=4.1)
Call: survfit(formula = my_survival ~ 1, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
4.1 1 7 0.29 0.216 0.0672 1Therefore, the survival at 4.1 years is 29%.
6. What is the median survival in Q4?
For the answer to this question we need to plot the survival curve:
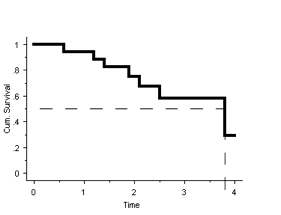
It can be seen from the graph that the median survival ≈ 3.75 years.
In R:
Alternatively, using the console method (as above):
my_curve
Call: survfit(formula = my_survival ~ 1, data = Q9, conf.int = 0.95)
n events median 0.95LCL 0.95UCL
[1,] 20 7 3.8 2.1 NATherefore, the median survival is 3.8 years.
7. Perform the Kaplan-Meier survival analysis in the worst-case scenario.
In the worst-case scenario, the patients lost to follow up count as a failure.
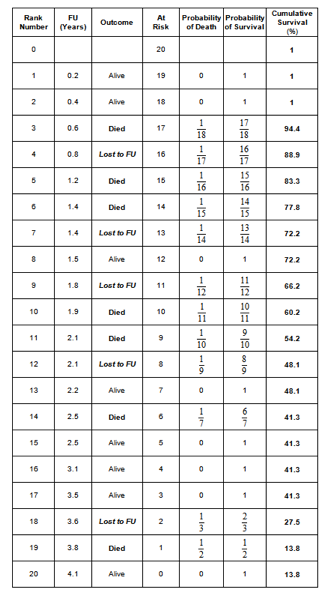
Similarly as in Q4, the ‘Outcome’ variable can be recoded into a new variable ‘Worst’; when the ‘Outcome’ is ‘alive’ ‘Worst’ is coded as 0 and when the ‘Outcome’ is ‘dead’ or ‘lost’ ‘Worst’ is coded as 1:
Q9$Worst <- ifelse(Q9$Outcome == 'alive', 0, 1)
Q9
Number FU Outcome Best Worst
1 1 0.2 alive 0 0
2 2 0.4 alive 0 0
3 3 1.5 alive 0 0
4 4 2.2 alive 0 0
5 5 2.5 alive 0 0
6 6 3.1 alive 0 0
7 7 3.5 alive 0 0
8 8 4.1 alive 0 0
9 9 0.6 dead 1 1
10 10 1.2 dead 1 1
11 11 1.4 dead 1 1
12 12 1.9 dead 1 1
13 13 2.1 dead 1 1
14 14 2.5 dead 1 1
15 15 3.8 dead 1 1
16 16 0.8 lost 0 1
17 17 1.4 lost 0 1
18 18 1.8 lost 0 1
19 19 2.1 lost 0 1
20 20 3.6 lost 0 1
str(Q9)
'data.frame': 20 obs. of 5 variables:
$ Number : num 1 2 3 4 5 6 7 8 9 10 ...
$ FU : num 0.2 0.4 1.5 2.2 2.5 3.1 3.5 4.1 0.6 1.2 ...
$ Outcome: Factor w/ 3 levels "alive","dead",..: 1 1 1 1 1 1 1 1 2 2 ...
$ Best : num 0 0 0 0 0 0 0 0 1 1 ...
$ Worst : num 0 0 0 0 0 0 0 0 1 1 ...Next perform the survival analysis as described above.
my_survival <- Surv(Q9$FU, Q9$Worst)
my_survival
[1] 0.2+ 0.4+ 1.5+ 2.2+ 2.5+ 3.1+ 3.5+ 4.1+ 0.6 1.2 1.4 1.9
[13] 2.1 2.5 3.8 0.8 1.4 1.8 2.1 3.6
summary(my_survival)
time status
Min. :0.200 Min. :0.0
1st Qu.:1.350 1st Qu.:0.0
Median :2.000 Median :1.0
Mean :2.035 Mean :0.6
3rd Qu.:2.650 3rd Qu.:1.0
Max. :4.100 Max. :1.0
my_curve <- survfit(my_survival ~ 1, data= Q9, conf.int=0.95)
summary(my_curve)
Call: survfit(formula = my_survival ~ 1, data = Q9, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0.6 18 1 0.944 0.0540 0.8443 1.000
0.8 17 1 0.889 0.0741 0.7549 1.000
1.2 16 1 0.833 0.0878 0.6778 1.000
1.4 15 2 0.722 0.1056 0.5423 0.962
1.8 12 1 0.662 0.1126 0.4743 0.924
1.9 11 1 0.602 0.1174 0.4107 0.882
2.1 10 2 0.481 0.1209 0.2944 0.788
2.5 7 1 0.413 0.1216 0.2316 0.735
3.6 3 1 0.275 0.1385 0.1026 0.738
3.8 2 1 0.138 0.1194 0.0251 0.754
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(my_curve, col='black', main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')
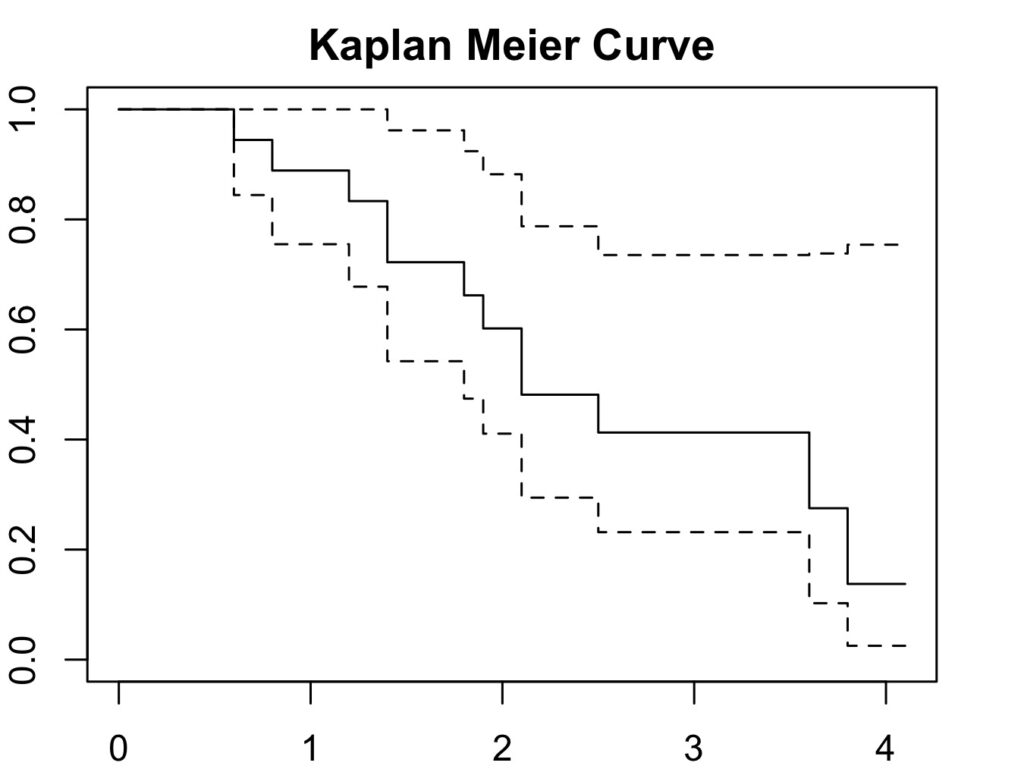
8. What is the survival in Q7 at 4.1 years?
Using the table in Q7: 13.8%.
Or alternatively in the console on the recoded variable ‘Worst’:
summary(my_curve,time=4.1)
Call: survfit(formula = my_survival ~ 1, data = Q9, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
4.1 1 12 0.138 0.119 0.0251 0.754Therefore, the survival at 4.1 years is 13.8%.
9. What is the median survival in Q7?
For the answer to this question we need to plot the survival curve:
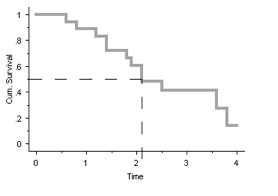
It can be estimated from the graph that the median survival ≈ 2.25 years.
In R:
my_curve
Call: survfit(formula = my_survival ~ 1, data = Q9, conf.int = 0.95)
n events median 0.95LCL 0.95UCL
[1,] 20 12 2.1 1.8 NATherefore, the median survival is 2.1 years.
The outcome data of 20 patients who had a total ankle replacement are listed in survivalankle.rda.
10. Calculate the 10-year Kaplan-Meier survival of the prosthesis using revision for aseptic loosening as ‘hard end point’.
Only patients who had a ‘Revision’ for aseptic loosening are counted as failures. The Kaplan-Meier table is as follows:
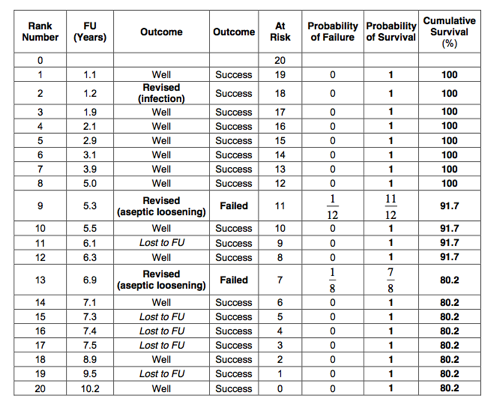
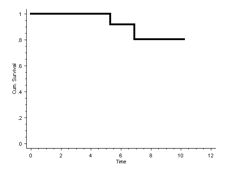
The 10-year Kaplan-Meier survival for aseptic loosening is therefore 80%:
In R:
First recode the ‘Outcome’ variable to a variable called ‘Censor’ as described above (Q4).
load("/path/to_file/survivalankle.rda")
survivalankle
Number FU Outcome
1 1 1.1 Well
2 2 1.2 Revised (infection)
3 3 1.9 Well
4 4 2.1 Well
5 5 2.9 Well
6 6 3.1 Well
7 7 3.9 Well
8 8 5.0 Well
9 9 5.3 Revised (aseptic loosening)
10 10 5.5 Well
11 11 6.1 Lost to FU
12 12 6.3 Well
13 13 6.9 Revised (aseptic loosening)
14 14 7.1 Well
15 15 7.3 Lost to FU
16 16 7.4 Lost to FU
17 17 7.5 Lost to FU
18 18 8.9 Well
19 19 9.5 Lost to FU
20 20 10.2 Well
survivalankle$Censor <- ifelse(survivalankle$Outcome == 'Revised (aseptic loosening)', 1, 0)
survivalankle
Number FU Outcome Censor
1 1 1.1 Well 0
2 2 1.2 Revised (infection) 0
3 3 1.9 Well 0
4 4 2.1 Well 0
5 5 2.9 Well 0
6 6 3.1 Well 0
7 7 3.9 Well 0
8 8 5.0 Well 0
9 9 5.3 Revised (aseptic loosening) 1
10 10 5.5 Well 0
11 11 6.1 Lost to FU 0
12 12 6.3 Well 0
13 13 6.9 Revised (aseptic loosening) 1
14 14 7.1 Well 0
15 15 7.3 Lost to FU 0
16 16 7.4 Lost to FU 0
17 17 7.5 Lost to FU 0
18 18 8.9 Well 0
19 19 9.5 Lost to FU 0
20 20 10.2 Well 0
survival_ankle <- Surv(survivalankle$FU, survivalankle$Censor)
summary(survival_ankle)
time status
Min. : 1.100 Min. :0.0
1st Qu.: 3.050 1st Qu.:0.0
Median : 5.800 Median :0.0
Mean : 5.460 Mean :0.1
3rd Qu.: 7.325 3rd Qu.:0.0
Max. :10.200 Max. :1.0
ankle_curve <- survfit(survival_ankle ~ 1, data=survivalankle, conf.int=0.95)
summary(ankle_curve)
Call: survfit(formula = survival_ankle ~ 1, data = survivalankle, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
5.3 12 1 0.917 0.0798 0.773 1
6.9 8 1 0.802 0.1279 0.587 1Plot the curve:
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(ankle_curve, col='black', main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')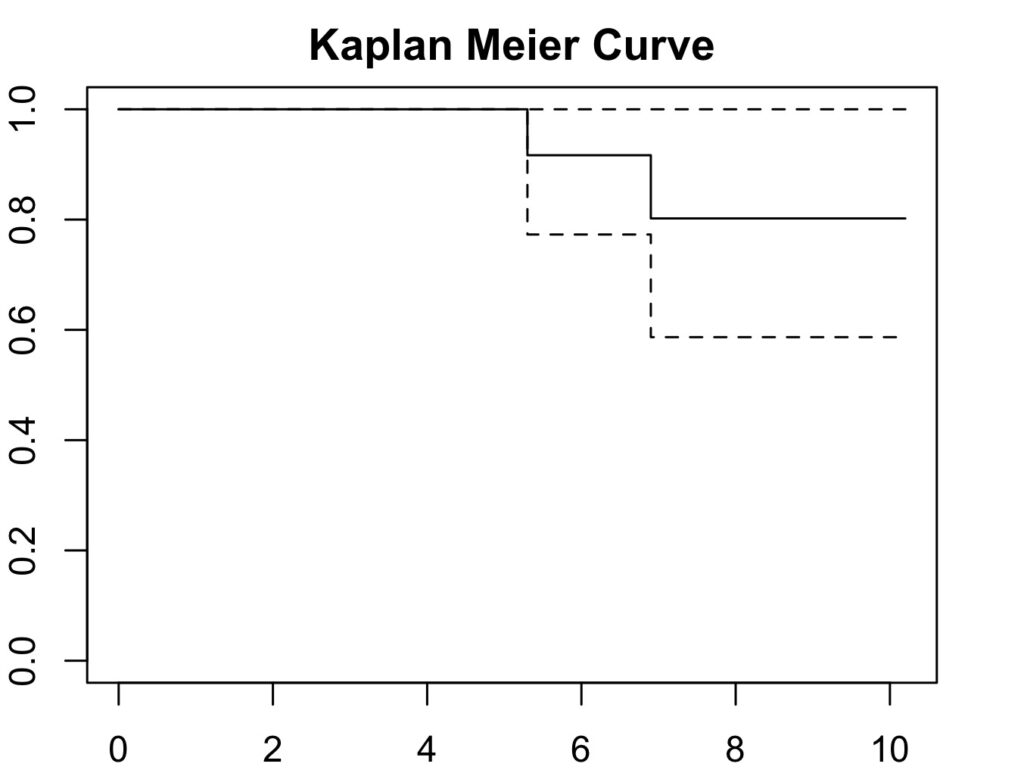
Therefore, the 10 year survival is 80%.
In the console:
summary(ankle_curve,time=10)
Call: survfit(formula = survival_ankle ~ 1, data = survivalankle, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
10 1 2 0.802 0.128 0.587 111. Calculate the 10-year Kaplan-Meier survival of the prosthesis using revision as ‘hard end point’.
All patients who had a ‘Revision’ are counted as failures. The Kaplan-Meier table is as follows:
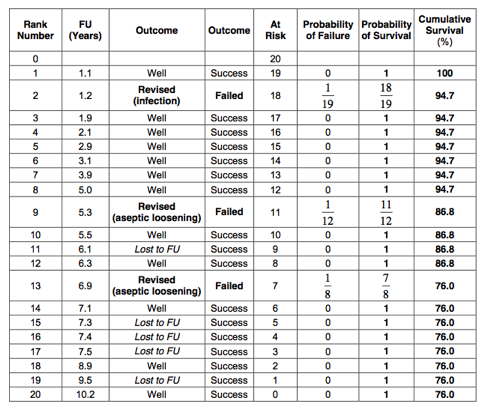
The 10-year Kaplan-Meier survival for revision is therefore 76%:
In R:
Perform recoding similar as to above into a new variable ‘Censor2’, but now counting all revisions as failures and perform the analysis.
survivalankle$Censor2 <- ifelse(survivalankle$Outcome == 'Revised (aseptic loosening)', 1, 0)
survivalankle$Censor2 <- ifelse(survivalankle$Outcome == 'Revised (infection)', 1, survivalankle$Censor2)
survivalankle
Number FU Outcome Censor Censor2
1 1 1.1 Well 0 0
2 2 1.2 Revised (infection) 0 1
3 3 1.9 Well 0 0
4 4 2.1 Well 0 0
5 5 2.9 Well 0 0
6 6 3.1 Well 0 0
7 7 3.9 Well 0 0
8 8 5.0 Well 0 0
9 9 5.3 Revised (aseptic loosening) 1 1
10 10 5.5 Well 0 0
11 11 6.1 Lost to FU 0 0
12 12 6.3 Well 0 0
13 13 6.9 Revised (aseptic loosening) 1 1
14 14 7.1 Well 0 0
15 15 7.3 Lost to FU 0 0
16 16 7.4 Lost to FU 0 0
17 17 7.5 Lost to FU 0 0
18 18 8.9 Well 0 0
19 19 9.5 Lost to FU 0 0
20 20 10.2 Well 0 0Survival analysis:
survival_ankle <- Surv(survivalankle$FU, survivalankle$Censor2)
survival_ankle
[1] 1.1+ 1.2 1.9+ 2.1+ 2.9+ 3.1+ 3.9+ 5.0+ 5.3 5.5+
[11] 6.1+ 6.3+ 6.9 7.1+ 7.3+ 7.4+ 7.5+ 8.9+ 9.5+ 10.2+
summary(survival_ankle)
time status
Min. : 1.100 Min. :0.00
1st Qu.: 3.050 1st Qu.:0.00
Median : 5.800 Median :0.00
Mean : 5.460 Mean :0.15
3rd Qu.: 7.325 3rd Qu.:0.00
Max. :10.200 Max. :1.00
ankle_curve <- survfit(survival_ankle ~ 1, data=survivalankle, conf.int=0.95)
summary(ankle_curve)
Call: survfit(formula = survival_ankle ~ 1, data = survivalankle, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1.2 19 1 0.947 0.0512 0.852 1
5.3 12 1 0.868 0.0890 0.710 1
6.9 8 1 0.760 0.1280 0.546 1Plot the curve:
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(ankle_curve, col='black', main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')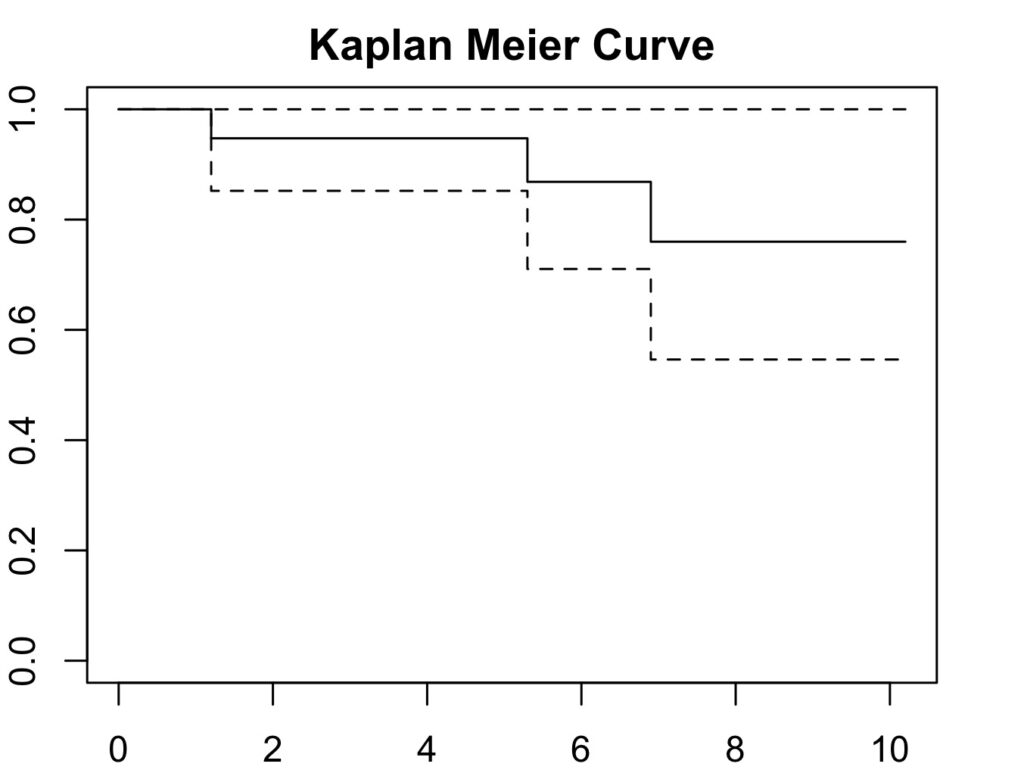
Therefore, the 10 year survival is 76%.
12. Calculate the 10-year worst-case scenario Kaplan-Meier survival of the prosthesis using revision as ‘hard end point’.
In the worst-case scenario, all patients who are lost to follow up are also counted as a failure:
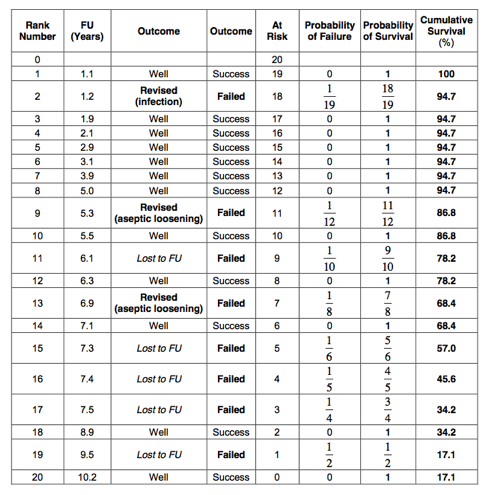
The worst-case scenario 10-year Kaplan-Meier survival for revision is therefore 17%:
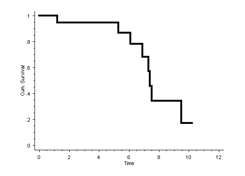
In R:
Again, perform recoding similar to above into a new variable called ‘Censor3’, now counting all revisions and all patients lost to follow up as a failure.
survivalankle$Censor3 <- ifelse(survivalankle$Outcome == 'Revised (aseptic loosening)', 1, 0)
survivalankle$Censor3 <- ifelse(survivalankle$Outcome == 'Revised (infection)', 1, survivalankle$Censor3)
survivalankle$Censor3 <- ifelse(survivalankle$Outcome == 'Lost to FU', 1, survivalankle$Censor3)
survivalankle
Number FU Outcome Censor Censor2 Censor3
1 1 1.1 Well 0 0 0
2 2 1.2 Revised (infection) 0 1 1
3 3 1.9 Well 0 0 0
4 4 2.1 Well 0 0 0
5 5 2.9 Well 0 0 0
6 6 3.1 Well 0 0 0
7 7 3.9 Well 0 0 0
8 8 5.0 Well 0 0 0
9 9 5.3 Revised (aseptic loosening) 1 1 1
10 10 5.5 Well 0 0 0
11 11 6.1 Lost to FU 0 0 1
12 12 6.3 Well 0 0 0
13 13 6.9 Revised (aseptic loosening) 1 1 1
14 14 7.1 Well 0 0 0
15 15 7.3 Lost to FU 0 0 1
16 16 7.4 Lost to FU 0 0 1
17 17 7.5 Lost to FU 0 0 1
18 18 8.9 Well 0 0 0
19 19 9.5 Lost to FU 0 0 1
20 20 10.2 Well 0 0 0Perform survival analysis:
survival_ankle = Surv(survivalankle$FU, survivalankle$Censor3)
survival_ankle
[1] 1.1+ 1.2 1.9+ 2.1+ 2.9+ 3.1+ 3.9+ 5.0+ 5.3 5.5+
[11] 6.1 6.3+ 6.9 7.1+ 7.3 7.4 7.5 8.9+ 9.5 10.2+
summary(survival_ankle)
time status
Min. : 1.100 Min. :0.0
1st Qu.: 3.050 1st Qu.:0.0
Median : 5.800 Median :0.0
Mean : 5.460 Mean :0.4
3rd Qu.: 7.325 3rd Qu.:1.0
Max. :10.200 Max. :1.0
ankle_curve <- survfit(survival_ankle ~ 1, data=survivalankle, conf.int=0.95)
summary(ankle_curve)
Call: survfit(formula = survival_ankle ~ 1, data = survivalankle, conf.int = 0.95)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1.2 19 1 0.947 0.0512 0.8521 1.000
5.3 12 1 0.868 0.0890 0.7104 1.000
6.1 10 1 0.782 0.1149 0.5859 1.000
6.9 8 1 0.684 0.1359 0.4633 1.000
7.3 6 1 0.570 0.1538 0.3358 0.967
7.4 5 1 0.456 0.1598 0.2294 0.906
7.5 4 1 0.342 0.1552 0.1404 0.833
9.5 2 1 0.171 0.1437 0.0329 0.888Plot the survival curve:
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(ankle_curve, col='black', main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')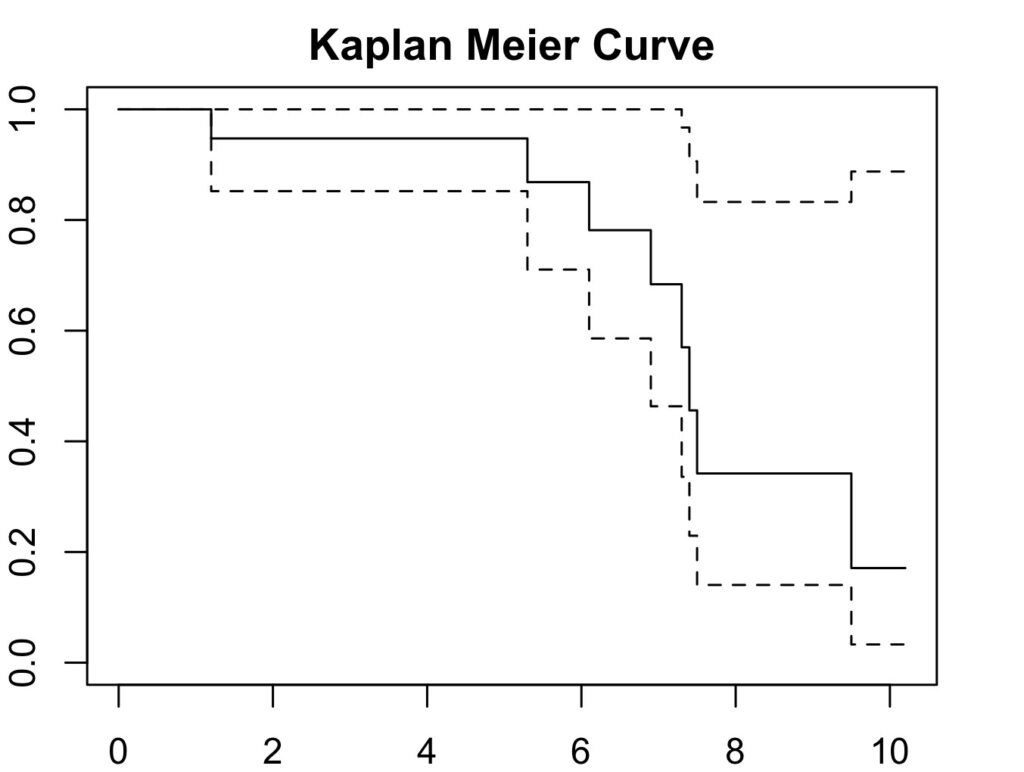
Again, giving the result 17%.
These questions illustrate the importance of choosing a ‘hard end point’. They also show that if all patients lost to follow up are counted as a failure (worst-case scenario), the survival curve drops steeply.
There was not much difference in the 10-year survival for ‘revision’ and ‘revision for aseptic loosening’. This is because the one patient who had an infection had this relatively early (at 1.2 years). At this time there were 18 patients who had a longer follow up. Consequently, the effect on the failure rate (1 out of 19) is not as big as it would have been if only 1 patient had a longer follow up (1 out of 2).
So, a failure at the ‘tail end’ (longer follow up) of the survival curve has a far more pronounced effect on the cumulative survival than a failure at the beginning (short follow up).
13. The plot can be created using console with the survival2 package .
Download the data and perform the analysis:
load("/path/to_file/survivalhip1.rda")
survivalhip1
Number FU Censor Group
1 1 5.1 FALSE Hip 1
2 2 6.4 TRUE Hip 1
3 3 7.8 TRUE Hip 1
4 4 8.2 TRUE Hip 1
5 5 9.3 TRUE Hip 1
6 6 10.4 FALSE Hip 1
7 7 10.5 TRUE Hip 1
8 8 10.7 FALSE Hip 1
9 9 10.9 TRUE Hip 1
10 10 11.1 FALSE Hip 1
11 11 4.6 FALSE Hip 2
12 12 5.2 FALSE Hip 2
13 13 6.9 FALSE Hip 2
14 14 7.6 FALSE Hip 2
15 15 8.1 FALSE Hip 2
16 16 8.4 FALSE Hip 2
17 17 8.9 FALSE Hip 2
18 18 9.7 TRUE Hip 2
19 19 10.6 TRUE Hip 2
20 20 11.3 FALSE Hip 2
hip_survival <- Surv(survivalhip1$FU, survivalhip1$Censor)
hip_survival
[1] 5.1+ 6.4 7.8 8.2 9.3 10.4+ 10.5 10.7+ 10.9 11.1+
[11] 4.6+ 5.2+ 6.9+ 7.6+ 8.1+ 8.4+ 8.9+ 9.7 10.6 11.3+
summary(hip_survival)
time status
Min. : 4.600 Min. :0.0
1st Qu.: 7.425 1st Qu.:0.0
Median : 8.650 Median :0.0
Mean : 8.585 Mean :0.4
3rd Qu.:10.525 3rd Qu.:1.0
Max. :11.300 Max. :1.0
hip_curve <- survfit(hip_survival ~ Group, data=survivalhip1, conf.int=0.95)
summary(hip_curve)
Call: survfit(formula = hip_survival ~ Group, data = survivalhip1,
conf.int = 0.95)
Group=Hip 1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
6.4 9 1 0.889 0.105 0.7056 1.000
7.8 8 1 0.778 0.139 0.5485 1.000
8.2 7 1 0.667 0.157 0.4200 1.000
9.3 6 1 0.556 0.166 0.3097 0.997
10.5 4 1 0.417 0.173 0.1847 0.940
10.9 2 1 0.208 0.171 0.0418 1.000
Group=Hip 2
time n.risk n.event survival std.err lower 95% CI upper 95% CI
9.7 3 1 0.667 0.272 0.2995 1
10.6 2 1 0.333 0.272 0.0673 1Plot the curve:
par(mar=c(2,2,2,2)) # to increase plot margins in RStudio
plot(hip_curve, col=c('red', 'blue'), main='Kaplan Meier Curve',
xlab='Follow Up Duration', ylab='Cumulative Survival Probability')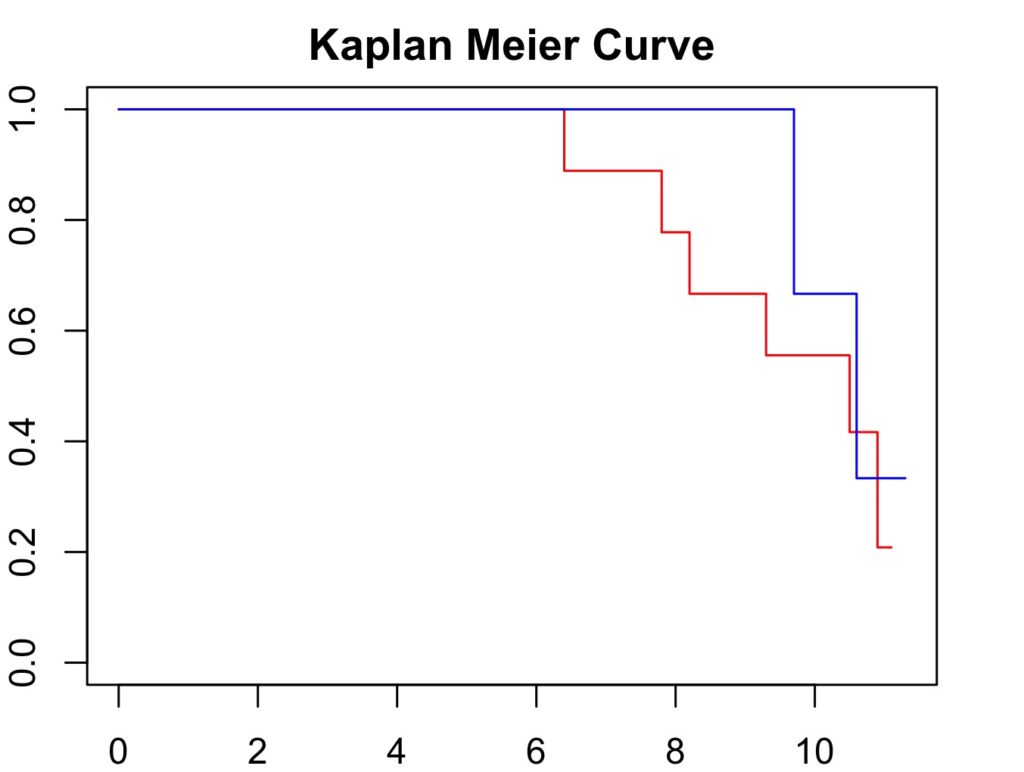
Hip 1 is red and Hip 2 is blue
R labels the curves alphabetically and it may be necessary to check which curve is which or add a legend (i.e. with the survminer3 package). From the output above, it can be seen that there were 6 failures in ‘Hip 1’ and two failures in ‘Hip 2’. Therefore, There should be 6 steps in the red curve and only two in the blue which is correct. The drops in the curve are steeper for ‘Hip 2’ because 7 patients were censored at the time of the first failure.
14. This can be done using the console and the survival package4.
Using the hip_survival object from question 13:
hip_survival <- Surv(survivalhip1$FU, survivalhip1$Censor)
hip_survival
[1] 5.1+ 6.4 7.8 8.2 9.3 10.4+ 10.5 10.7+ 10.9 11.1+
[11] 4.6+ 5.2+ 6.9+ 7.6+ 8.1+ 8.4+ 8.9+ 9.7 10.6 11.3+
summary(hip_survival)
time status
Min. : 4.600 Min. :0.0
1st Qu.: 7.425 1st Qu.:0.0
Median : 8.650 Median :0.0
Mean : 8.585 Mean :0.4
3rd Qu.:10.525 3rd Qu.:1.0
Max. :11.300 Max. :1.0
Perform the logrank test:
hip_logrank <- survdiff(hip_survival ~ Group, data=survivalhip1)
hip_logrank
Call:
survdiff(formula = hip_survival ~ Group, data = survivalhip1)
N Observed Expected (O-E)^2/E (O-E)^2/V
Group=Hip 1 10 6 4.91 0.242 0.634
Group=Hip 2 10 2 3.09 0.385 0.634
Chisq= 0.6 on 1 degrees of freedom, p= 0.4 Perform Cox Proportional Hazards:
hip_coxph <- coxph(hip_survival ~ Group, data=survivalhip1)
hip_coxph
Call:
coxph(formula = hip_survival ~ Group, data = survivalhip1)
coef exp(coef) se(coef) z p
GroupHip 2 -0.642 0.526 0.820 -0.78 0.43
Likelihood ratio test=0.67 on 1 df, p=0.412
n= 20, number of events= 8 And parametric Weibull:
hip_parametric <- survreg(hip_survival ~ Group , dist = "weibull",
data=survivalhip1)
hip_parametric
Call:
survreg(formula = hip_survival ~ Group, data = survivalhip1,
dist = "weibull")
Coefficients:
(Intercept) GroupHip 2
2.36525220 0.08988363
Scale= 0.1416005
Loglik(model)= -20.5 Loglik(intercept only)= -20.8
Chisq= 0.66 on 1 degrees of freedom, p= 0.416
n= 20 Similarly, perform the exponential parametric test which should show the following output (parts omitted for brevity):
hip_parametric <- survreg(hip_survival ~ Group , dist = "exponential",
data=survivalhip1)
hip_parametric
Call:
survreg(formula = hip_survival ~ Group, data = survivalhip1,
dist = "exponential")
Coefficients:
(Intercept) GroupHip 2
2.712485 0.992514
Scale fixed at 1
Loglik(model)= -31.7 Loglik(intercept only)= -32.5
Chisq= 1.69 on 1 degrees of freedom, p= 0.193
n= 20There is no statistical significant difference using the log rank test (p=0.42), cox proportional hazards model (p=0.412) and parametric regression analysis using the exponential (p=0.193) and Weibull (p=0.416) distributions between the survival curves of both hips. Therefore, the null hypothesis can’t be rejected and it should be concluded that there is no difference in the outcome of both hips.