If we want to use a t-test to analyse our data, it is necessary to demonstrate the data are Normally distributed. Many tests for Normality have been described and it is not in the scope of this book to discuss them all. However, three different tests will be discussed:
- Quantile-Quantile plots
- Shapiro-Wilk test
- Kolmogorov-Smirnov test
Two data sets will be used in the discussion of all three Normality tests:
After downloading the data, they can be shown in the R console by:
height10$height
[1] 184 146 169 185 160 173 179 171 160 150
tibfracture10$healingtime
[1] 24 55 19 20 36 11 25 18 10 16
Descriptives can be obtained by:
descriptive.table(vars = d(height),data= height10, func.names =c(“Mean”,”Median”,”St. Deviation”,”Valid N”,”Minimum”,”Maximum”))
$`strata: all cases `
Mean.height Median.height St. Deviation.height Valid N.height Minimum.height Maximum.height
167.70000 170.00000 13.48291 10.00000 146.00000 185.00000
descriptive.table(vars = d(healingtime),data= tibfracture10, func.names =c(“Mean”,”Median”,”St. Deviation”,”Valid N”,”Minimum”,”Maximum”))
$`strata: all cases `
Mean.healingtime Median.healingtime St. Deviation.healingtime Valid N.healingtime Minimum.healingtime
23.40000 19.50000 13.36829 10.00000 10.00000
Maximum.healingtime
55.00000
or
summary(height10$height)
Min. 1st Qu. Median Mean 3rd Qu. Max.
146.0 160.0 170.0 167.7 177.5 185.0
sd(height10$height)
[1] 13.48291
summary(tibfracture10$healingtime)
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.00 16.50 19.50 23.40 24.75 55.00
sd(tibfracture10$healingtime)
[1] 13.36829
The mean and median for height are close together (167.7 and 170 respectively), suggesting that the heights may be normally distributed. However, the mean and median for the fracture healing times are further apart (23.4 and 19.5 respectively) making it less likely that this is normally distributed.
Graphical normality test (quantile-quantile plot)
This graphical test is probably the easiest way to test for Normality. However, it is a graphical (visual assessment) test and a p value is not obtained. The method creates a plot from the ranked samples of our data against a similar number of ranked theoretical samples from a Normal distribution. If it shows a straight line, the data is Normally distributed. Otherwise, if the data deviates from a straight line, the distribution is not Normal. In the JGR console window enter:
qqnorm(height10$height)
qqline(height10$height,lty=2)
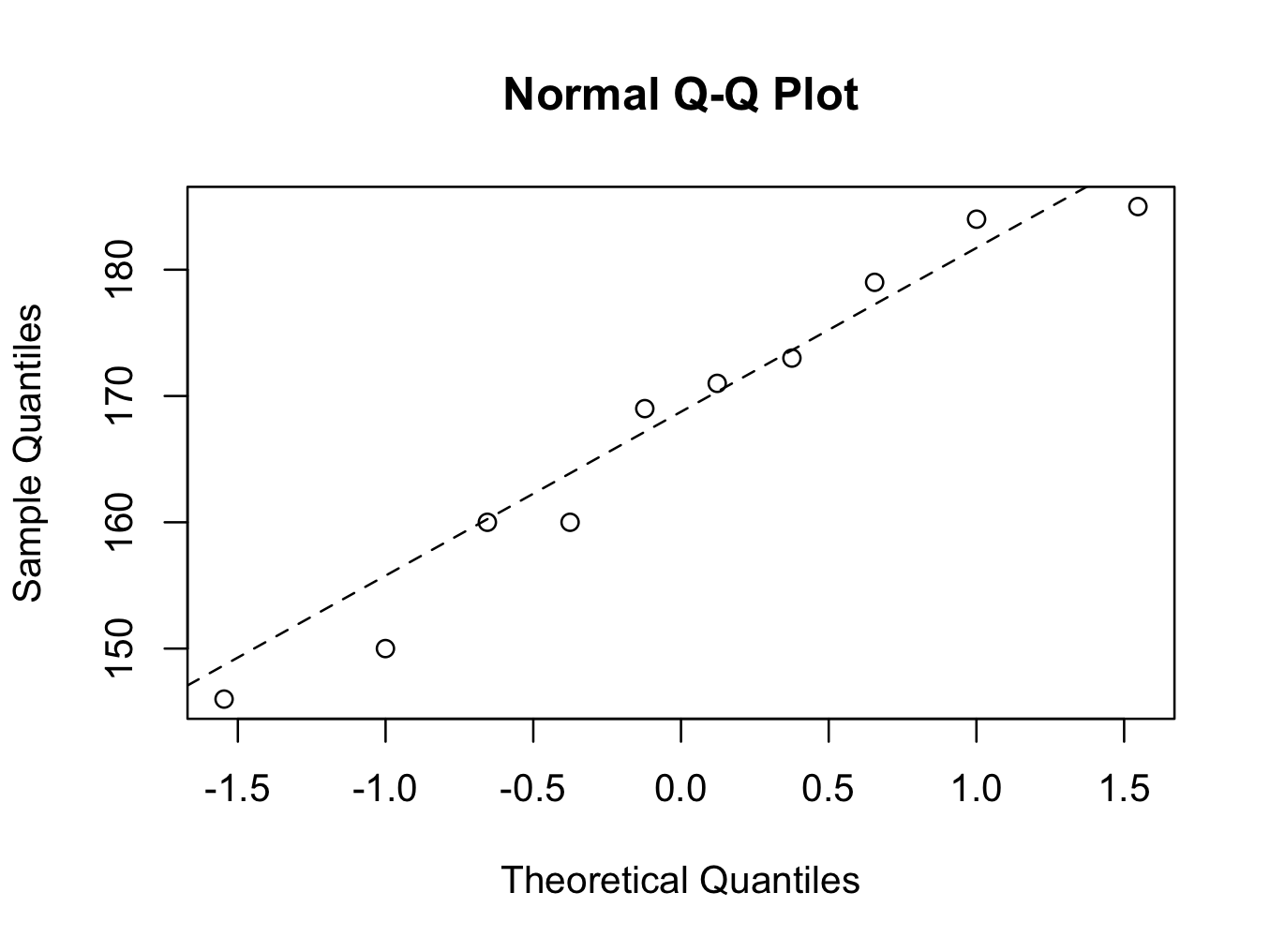The first command creates the plot and the second command draws the reference line. The parameter ‘lty=2′ is optional and creates a dotted line instead of an uninterrupted line. The data points are near enough the straight line and it is therefore reasonable to assume the data are Normally distributed using the QQ plot method.
The same for the tibial fracture healing times:
qqnorm(tibfracture10$healingtime)
qqline(tibfracture10$healingtime,lty=2)
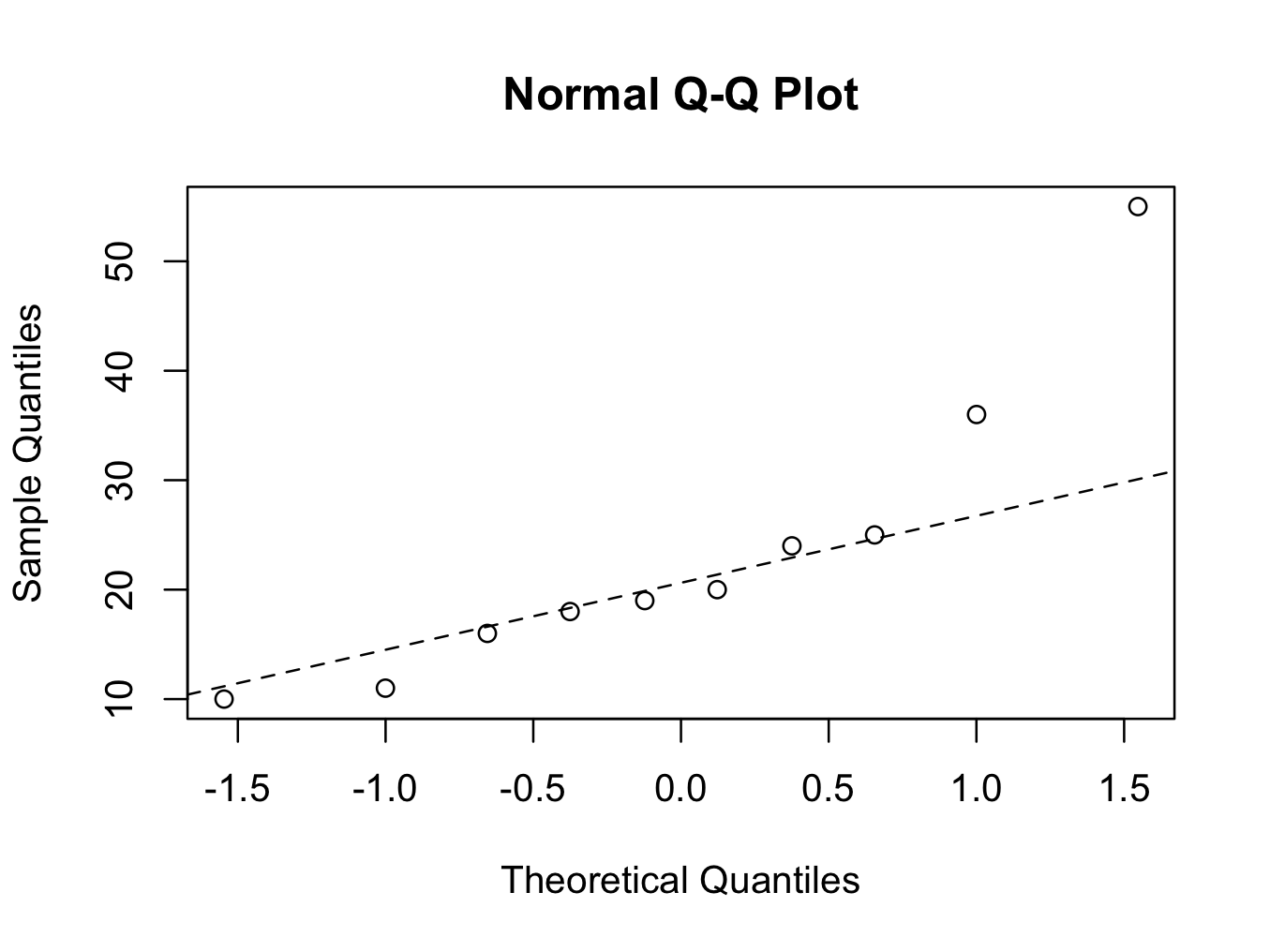The second plot clearly shows that the data points for tibial fracture healing time are deviating from the straight line. The fracture healing time is therefore not Normally distributed (using the quantile-quantile plot method).
Shapiro-Wilk Normality test
The Shapiro-Wilk test estimates whether data are from a normal distribution. It is particular useful in smaller sample sizes (<2000). The null hypothesis is that the data are from a normal distribution. The alternate hypothesis is that the data are not normally distributed.
The Shapiro-Wilk test can be performed in Deducer by selecting Analysis and then One Sample Test:
This will perform a one-sample t-test. In the dialogue screen, ascertain the ‘Shapiro-Wilk test against normality’ is ticked. Select the appropriate variable and click run.
This will give the following output for the height data:
one.sample.test(variables=d(height), data=height10, test=t.test, alternative=”two.sided”)
One Sample t-test
mean of x 95% CI Lower 95% CI Upper t df p-value
height 167.7 158.0549 177.3451 39.3323 9 2.207089e-11
HA: two.sided
H0: mean = 0
one.sample.test(variables=d(height), data=height10, test=shapiro.test)
Shapiro-Wilk normality test
W p-value
height 0.9444367 0.6033499
And for the healing time data:
one.sample.test(variables=d(healingtime), data=tibfracture10, test=t.test, alternative=”two.sided”)
One Sample t-test
mean of x 95% CI Lower 95% CI Upper t df p-value
healingtime 23.4 13.8369 32.9631 5.535286 9 0.0003632489
HA: two.sided
H0: mean = 0
one.sample.test(variables=d(healingtime), data=tibfracture10, test=shapiro.test)
Shapiro-Wilk normality test
W p-value
healingtime 0.8395738 0.04360842
Alternatively, to just perform a Shapiro-Wilk tests in the console:
shapiro.test(height10$height)
Shapiro-Wilk normality test
data: height10$height
W = 0.9444, p-value = 0.6033
shapiro.test(tibfracture10$healingtime)
Shapiro-Wilk normality test
data: tibfracture10$healingtime
W = 0.8396, p-value = 0.04361
gives the same answers.
The p-value of the Shapiro-Wilk test for the height variable is 0.6033 and not significant. Therefore, there is no reason to reject the null hypothesis and it can be concluded that it is reasonable to regard the height data as Normally distributed.
The p-value for the healing time however is 0.04361, which is significant. Therefore, we reject the null hypothesis in favour of the alternative hypothesis and conclude the data are not Normally distributed. Consequently, the t-test should not be used for analysis, but non-parametric analysis should be used instead.
Kolmogorov-Smirnov Normality test
The Kolmogorov-Smirnov ‘goodness to fit’ test examines whether two datasets differ significantly. It makes no assumption on the distribution of the data and is technically speaking a non-parametric test. It can also be used to demonstrate that the data fit other distributions (outside the scope of this book). However, because the Kolmogorov-Smirnov test is more general, it tends to be less powerful (larger numbers are required to note a difference). The test is especially useful in larger sample sizes (> 50). The null hypothesis is that the data follow the specified distribution and the alternative hypothesis is that the data are not from the same distribution. To test whether the height data are normally distributed enter in the command window:
ks.test(height10$height,”pnorm”,mean=mean(height10$height),sd=sd(height10$height))
One-sample Kolmogorov-Smirnov test
data: height10$height
D = 0.1384, p-value = 0.9909
alternative hypothesis: two-sided
Warning message:
In ks.test(height10$height, “pnorm”, mean = mean(height10$height), :
ties should not be present for the Kolmogorov-Smirnov test
The Kolmogorov-Smirnov test compares the height data with a Normal distribution (“pnorm”) that has a mean and standard deviation that is the same as the height data (mean =mean(height10$height) and sd=sd(height10$height)). The p -value is 0.9909 and there is no reason to reject the null hypothesis (there is no difference between the height data and a normal distribution with the same mean and standard deviation). It can be concluded that the height is Normally distributed using the Kolmogorov-Smirnov test for Normality.
The output does state that a correct p-value can’t be computed with ties (the same values in the data). This is because two of the ten patients have a height of 160 cm. This can easily be overcome by introducing a greater precision into the data
height=c(184,146,169,185,160,173,179,171,160.001,150)
Now, the test gives a more accurate p-value:
ks.test(height,”pnorm”,mean=mean(height),sd=sd(height))
One-sample Kolmogorov-Smirnov test
data: height
D = 0.1384, p-value = 0.9769
alternative hypothesis: two-sided
Please note that a new variable height has been declared that is different from the height variable in the height10 data frame. As a result, only height is entered as argument for the function and not height10$height.
To test the fracture healing time data with the Kolmogorov-Smirnov test:
ks.test(tibfracture10$healingtime,”pnorm”,mean=mean(tibfracture10$healingtime),sd=sd(tibfracture10$healingtime))
One-sample Kolmogorov-Smirnov test
data: tibfracture10$healingtime
D = 0.2524, p-value = 0.4723
alternative hypothesis: two-sided
On the basis of the Kolmogorov-Smirnov test, the null hypothesis (there is no difference between the healing time data and a Normal distribution with a the same mean and standard deviation) can’t be rejected. The conclusion that the data is Normally distributed seems reasonable. However, the graphical method and the Shapiro-Wilk test have shown that the healing time is not Normally distributed. This illustrates the lesser statistical power of the Kolmogorov-Smirnov test, especially in smaller sample sizes.