Following statistical analysis, it can be concluded whether the difference is statistically significant or not. Depending on that, we either accept or reject the null hypothesis. This decision could be correct or wrong.
α is the probability of rejecting the null hypothesis, when in fact it is true (false positive). We usually set this significance level at 5%.
β is the probability of incorrectly accepting the null hypothesis (false negative).
The power is the probability the test will correctly reject the null hypothesis. Therefore: Power = 1 – β
There are two types of errors:
Type 1 Error (or error of the first kind):
The null hypothesis is incorrectly rejected. When the null hypothesis is rejected, we have concluded that there is a difference. However, this is incorrect (there really is no difference). A type 1 error therefore, could be regarded as a false positive. We can reduce the risk of a type one error by reducing the significance level (α).
Type 2 Error (or error of the second kind):
The null hypothesis is incorrectly accepted. When the null hypothesis is accepted, we have concluded there is no difference. However, this is incorrect (there is a difference). A type 2 error therefore, is a false negative. It is controlled with the Statistical Power (β)
The probability of making a type 1 error can be reduced by decreasing α (usually set a at 5%). However, in doing so we increase the probability of making a type 2 error! The graph below shows two Normal distributions with a standard deviation of 0.5. The left curve has a mean of 0 and the right of 3:
The graph below shows two Normal distributions with a standard deviation of 2. The left curve has a mean of 0 and the right of 3:
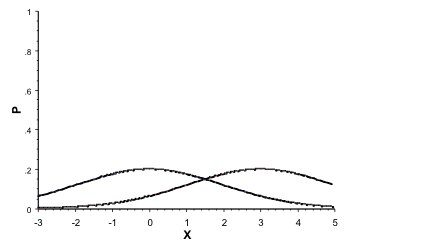Looking at these graphs, it becomes obvious that errors are related to:
- Difference desired to detect. If the difference in means is larger, an error is less likely.
- Spread of data. The larger the dispersion of the data, the more likely an error is committed. A large variance (or standard deviation) or range indicates more dispersion.
- Significance level (α). Selecting a lower significance level reduces the probability to commit a type 1 error. However, a type 2 error becomes more likely.
- Test statistic (power). By selecting a more powerful test (such as a parametric test), a type 2 error is less likely.