Normal Distribution | Stats Book

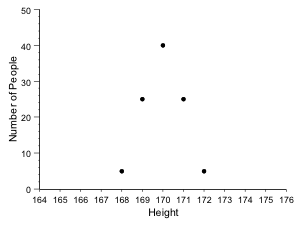
Suppose we measured the heights of 100 people to the nearest centimetre. The measured variable is called ‘Height’ and there are 100 variates (individual measurements). The number of observations is n = 100 and are summarised in the table below:

Height	Number or People
Total	100
168	5
169	25
170	40
171	25
172	5

The data can also be plotted:

If the data points are connected, a distribution plot is obtained:

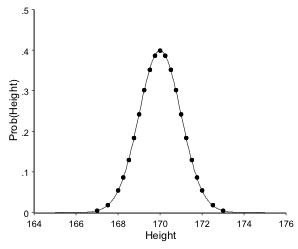
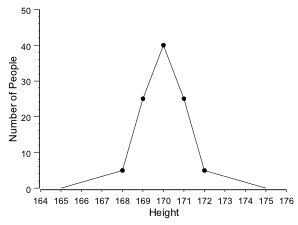If the measurements would have been in millimetres rather than centimetres, the curve becomes smooth:

This graph shows the distribution of the variable Height.

Also note that the y-axis now shows the probability rather than the actual number of people. This curve is called the Gaussian or ‘bell shaped’ curve.

The curve has the following basic formula:

$Height=\frac{1}{\sqrt{2\pi}}exp\left ( \frac{x^2} {2}\right )$

Further mathematics is beyond the scope of this book.

However, if data are distributed according to this formula, the data are called Normally distributed. Any other distribution of data is called a not Normal. If the distribution of the data is according to a described formula (ie Normal), parametric statistical analysis can be used to analyse the data. However, if the data are not distributed according to a described distribution, non parametric analysis should be used.

Mean

Returning to the example, the mean height can be calculated:

$Mean(Height)=\frac{5\times168+25\times169+40\times170+25\times171+5\times172}{100}=170$

As can be seen, the mean is at the top of the Gaussian curve.

The curve is symmetrical around the mean.

In general terms, the mean is:

$Mean(x)=\frac{1}{n} \sum_{i=1}^{n} x(i)$

The mean and average are often used as synonyms. However, they are not quite the same. The mean is an average, but there are other averages than the mean (such as mode and median).

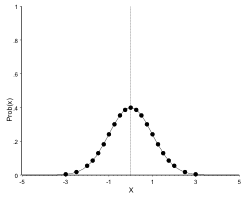
A Normal distribution with mean zero and standard deviation of 1:

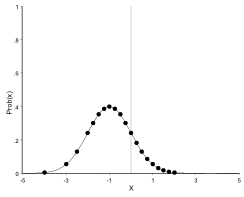
The same distribution with mean -1:

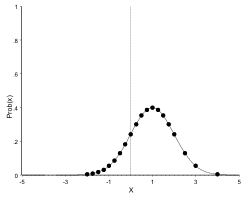
And with mean +1:

As can be seen, the distribution curve shifts to the left when the mean decreases and to the right when the mean increases. The shape of the curve however, remains unchanged: A different mean shifts the curve along the x-axis, but does not alter its shape.

Standard Deviation and Variance

In describing normally distributed data, the standard deviation and variance are used. They are a measure of the spread (or variability) of the data.

The variance is the standard deviation (S) squared or:

$Variance=\sigma^2$

$\sigma=\sqrt{Variance}$

In general terms:

$Variance(X 1)=\frac{1}{n-1}\sum_{i=1}^{n} (X1(i)-Mean(X1)) ^{2}$

The term $\sum_{i=1}^{n} (X1(i)-Mean(X1)) ^{2}$ is the sum of the squares about the mean.

Returning to the example (with mean 170 cm), the sum of the squares about the mean is:

$\sum_{i=1}^{n} (Height(i)-Mean(Height))^2$ = $5\times(168-170)^2+25\times(169-170)^2+40\times(170-170)^2+25\times(171-170)^2+5\times(172-170)^2$ = $5\times(-2)^2+25\times(-1)^2+40\times(0)^2+25\times(1)^2+5\times(2)^2$ = $5\times4+25\times1+40\times0+25\times1+5\times4$ = $20+25+25+20=90$

So the variance is:

$Variance=\frac{1}{100-1}\times90\approx 0.91$

And the standard deviation is:

$StandardDeviation=\sqrt{0.91}\approx 0.95$

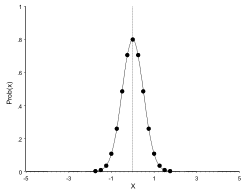
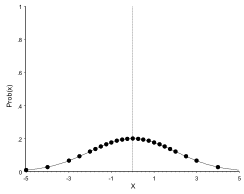
Again, lets look at a Normal distribution with a mean of zero and a standard deviation of 1:

The same distribution, but with standard deviation 0.5:

And with standard deviation 2:

So the standard deviation is a measure of the spread (or variability of the data). When the standard deviation decreases, the curve becomes steeper (data closer together). When the standard deviation increases, the curve becomes flatter (data further spread apart).

If the data are normally distributed, the distribution of data can be described by two parameters: the mean and the standard deviation (or variance).

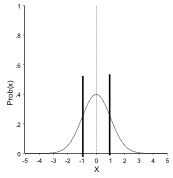
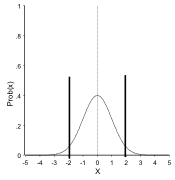
As stated above, the standard deviation is a measure of the spread of data. It can be shown that 68.27% of the data lie in an interval plus or minus one standard deviation from the mean. Similarly 95.45% of the data lie in an interval plus or minus twice the standard deviation and 99.73% of the data within an interval plus or minus three times the standard deviation.

Or:

Mean + / – 1 × SD = 68 %

Mean + / – 2 × SD = 95 % (more accurately 1.96 times the SD)

Mean + / – 3 × SD = 99 %

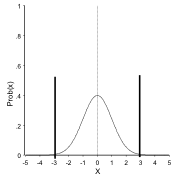
This is shown in graphs below.

Mean + or – 1 times standard deviation (68% of the data in interval):

Mean + or – 2 times standard deviation (95% of the data in interval):

Mean + or – 3 times standard deviation (99% of the data in interval):

In our example, the Mean was 170 and the standard deviation was 0.95.

Therefore:

68% of the data are between 169.05 and 170.95

95% of the data are between 168.1 and 171.9

99% of the data are between 167.15 and 172.85