Mr Paul Cool & Prof Jan C Cool*
Friday the 13th is considered to be an unlucky day. It is also suggested that the occurrence of this combination is unusual. But is this the case? Is the 13th of the month less likely or more likely to fall on a Friday than any other day? Or is it evenly distributed? The answer to this question will be examined in this short paper.
Why Friday the 13th is considered to be unlucky is not quite certain. However, it has been suggested that this dates back to Jacques de Molay (1244-1314), who was the 23rd and last grand master of the Knights Templar. The knights Templar were officially endorsed by the Catholic Church in the middle ages and became very influential, wealthy and powerful. The Knights Templar played a prominent role in the crusades. However, when the holy land was lost, support for the order diminished in the late 13th century. King Philip IV of France was hugely in debt to the order and had Jacques de Molay as well as other prominent Knight Templars arrested on Friday 13th October 1307. The Templars were subsequently tortured into making false confessions. Under pressure of King Philip IV, pope Clement V disbanded the order in 1312. Although Jacques de Molay retracted his earlier confession, he was burned on an island in the river Seine in Paris in March 1314.
 During his execution in March 3014, de Molay cursed Philip IV and pope Clement V to follow him within a year.
During his execution in March 3014, de Molay cursed Philip IV and pope Clement V to follow him within a year.
During his execution, de Molay cursed both Philip IV of France and pope Clement V to follow him within a year. Both indeed died in 1314. Jacques de Molay ended up as a legendary figure. It may be that this is the reason that Friday 13th, the day of de Molay’s arrest, is deemed unlucky. It also seems implicit that Friday the 13th is an uncommon occurrence. But is this the case?
The history of our calendar is complex and beyond the scope of this paper. The calendar is based on the cycle of the moon. In early Roman calendars, there were only 10 months (Martius, Aprilis, Majus, Junius, Quintilis, Sextilis, Septembris, Octobris, Novembris, Decembris). There were 6 months of 30 days and 4 of 31 days. A year therefore, lasted 304 days. A tropical year however, lasts 365.2422 days and consequently the seasons became out of sink.
The solution to this problem was the Julian calendar that was introduced in 45 BC by Julius Caesar. Two additional months (January and February) were created. February had 29 days. All other months were 30 or 31 days long. A leap day was added to February every four years. An average Julian calendar year therefore lasts 365.25 days.
Quintilis became July. Later, Sextilis was renamed August in honour of Caesar Augustus and a day was taken from February to make Augustus the same number of days as July.
As a tropical year (365.2422 days), is slightly shorter than the average calendar year, the Julian calendar did not quite compensate for the difference. Consequently, the calendar gained approximately three days every four centuries. This was corrected with the introduction of the Gregorian calendar in 1582 by pope Gregory XIII. Leap years in the Gregorian calendar have the following rule:
if year is divisible by 400 then
is_leap_year
else if year is divisible by 100 then
not_leap_year
else if year is divisible by 4 then
is_leap_year
else not_leap_year
The Gregorian calendar has now been universally adopted as the civil calendar. However, some orthodox churches continue to use the Julian calendar. The Julian calendar is currently 14 days ahead of the Gregorian calendar.
The Gregorian calendar repeats itself every four hundred years. In this 400-year period, there are 303 regular years and 97 leap years. An average calendar year therefore is:
365 + ¼ -1/100 +1/400 = 365.2425 days.
This is still not quite synchronous with the solar time. Therefore, on occasion one-second adjustments, called leap seconds, are applied to the Universal Coordinated Time.
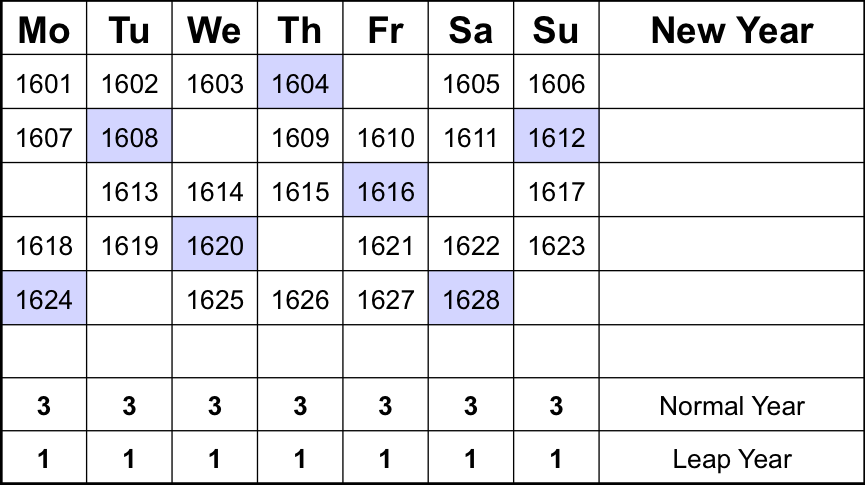
How does the Gregorian calendar repeat itself every 400 years? To examine this, we start on Monday the 1st January 1601. This was a normal year with 365 days. As a week has seven days and there is a leap year every four years, the repeat period of the calendar is 28 years. So, after 28 years you could use the same calendar again. This is from 1629 onwards in our example. There are two further identical repeat periods of 28 years (1657 and 1685).
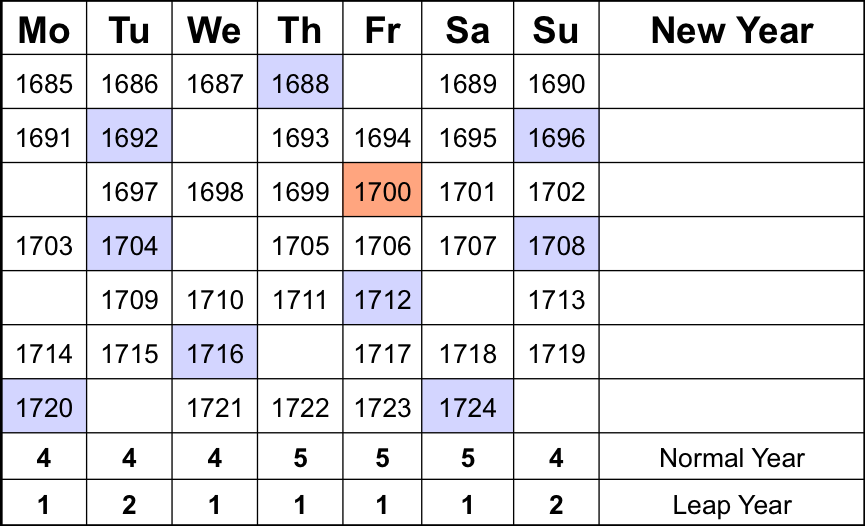
However, 1700 was not a leap year, and now it takes 40 years (from 1685) for the calendar to come back to its repeat cycle. This is in 1725, as illustrated in the table below:
Repeat periods
1601 1821
28 A 28
1629 1849
28 28
1657 1877
28 40 D
1685 1917
40 B 28
1725 1945
28 28
1753 1973
28 28 A
1781 2001
40 C
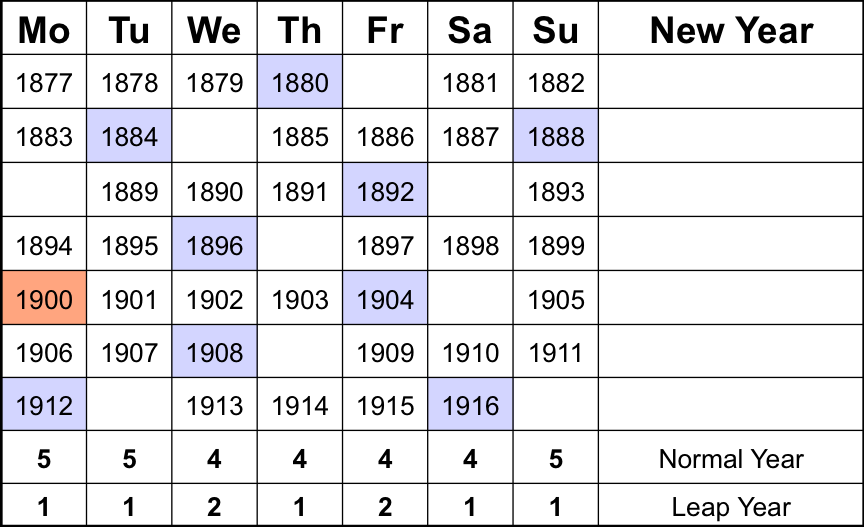
After two 28-year repeat periods, the next century year (1800) is not a leap year and it takes again 40 years for the calendar to return to its 28-year cycle. As can be seen in the table, there is a further period of 40 years around 1900. The year 2000 however, was not a leap year, and consequently the repeat period around the turn of the millennium was 28 years.
Therefore, there are four different repeat periods:
- Period A: 28 year repeat period
- Period B: 40 year repeat period around 1700
- Period C: 40 year repeat period around 1800
- Period D: 40 year repeat period around 1900
In first 28-year repeat period is illustrated in the table below:
The table shows on what day New Years Day falls. Leap years are highlighted in blue. The other 28-year repeat periods are identical (i.e. from 1629 to 1657).
The other periods of interest are the 40-year repeat period B around 1700 (century year highlighted in red), period C around 1800 and period D around 1900.
Period B around 1700:
Period C around 1800:
Period D around 1900:
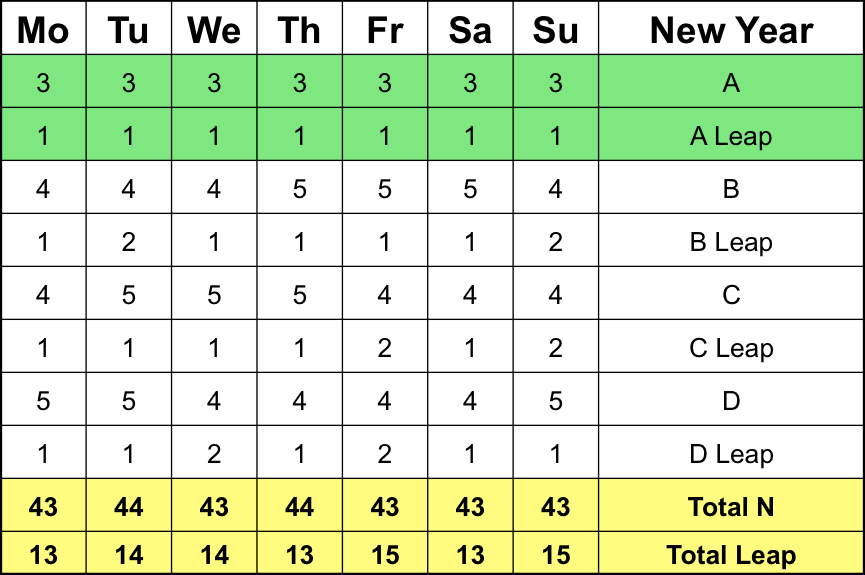
A 400-year period consists of 10 periods A of 28 years and 3 40-year periods (period B, C, D).
In period A, New Year’s Day falls four times on a Monday; three times during a normal year and once in a leap year. In period B and C, New Year’s Day falls four times on a Monday during a normal year and once during a leap year. In period D however, New Year’s Day falls five times on a Monday during a normal year and once during a leap year.
Grouping this together over 400 years for all days gives the following table:
The table give the occurrence of New Year’s Day on a specific day in the 400-year period the calendar repeats itself. It can be seen that the distribution of days is not quite even.
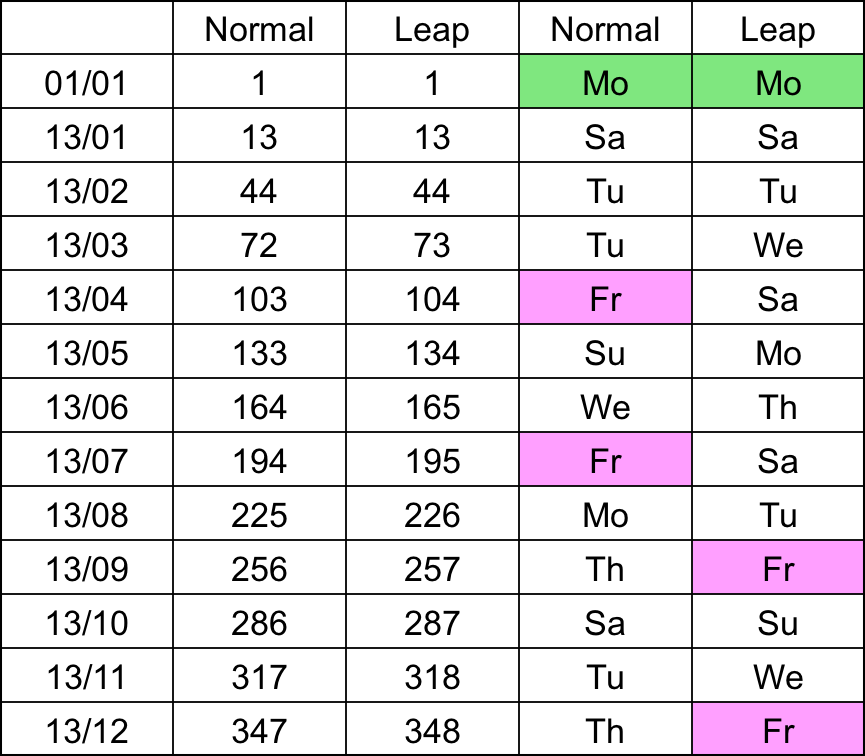
When New Year’s Day falls on a Monday, the 13th of January falls on a Saturday and the 13th of February (day 44 of the year) on a Tuesday. However, the 13th of March falls on a Tuesday during a normal year and a Wednesday in a leap year. This is summarized for the 13th of each month in the table below:
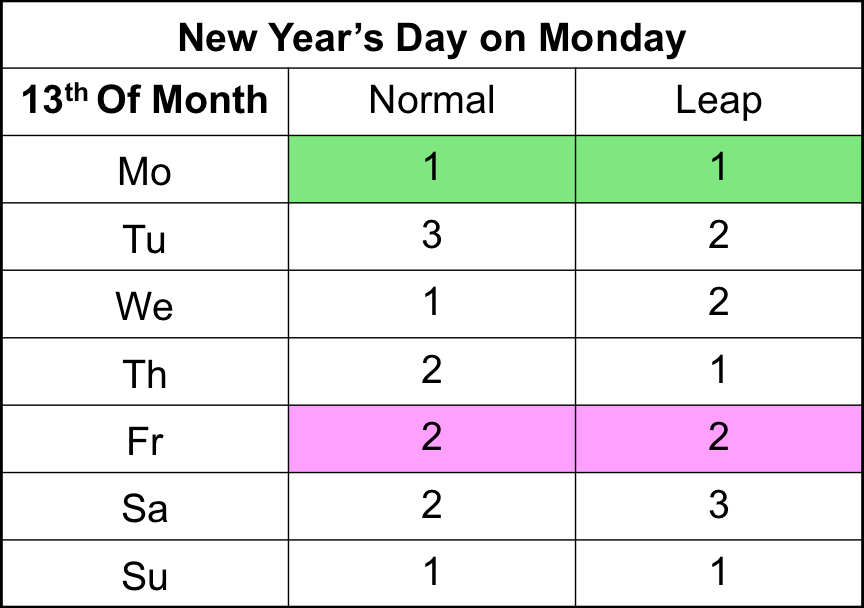
Therefore, if New Year’s Day falls on a Monday, there are two Friday the 13th during a normal year (13th April and 13th July) and two during a leap year (13th September and 13th December).
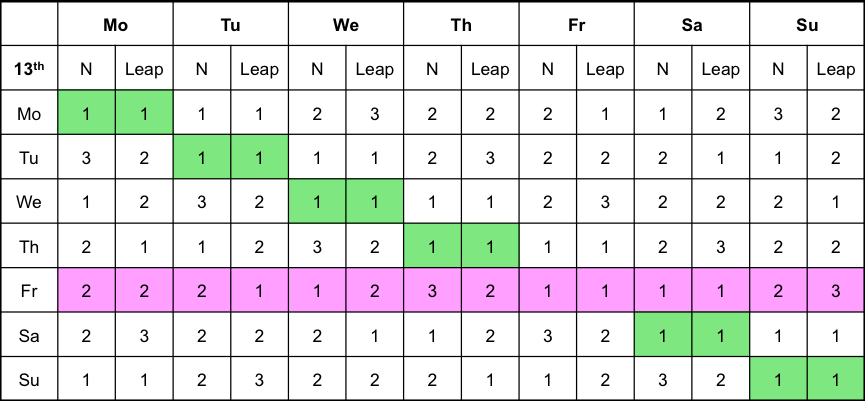
The same can be calculated when New Year’s Day fall on the other days of the week. This is summarized in the table below:
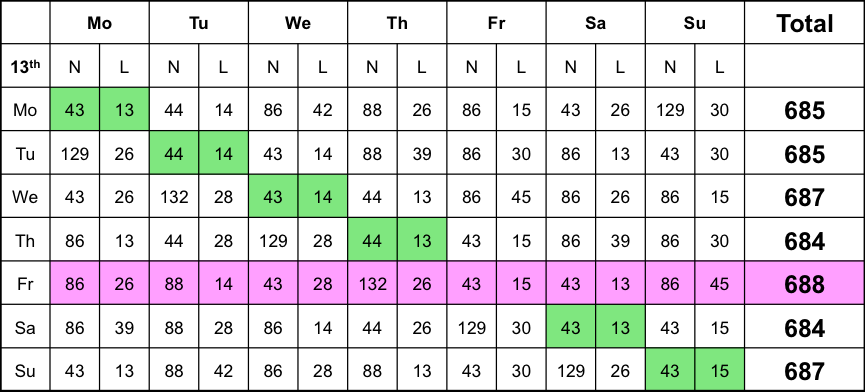
As was calculated above, over the 400-year repeat period, New Year’s Day falls 43 times on a Monday during a normal year and 13 during a leap year and so on. Therefore, summarizing over 400 years:
As can be seen from the table, over the 400 years, the 13th of the month falls 688 times on a Friday. This is more than any other combination and the 13th of the month more frequently falls on a Friday than on any other day!
Similar calculations can be done for every day of the month. It can be shown that the 1st of the month most commonly falls on a Sunday, the 2nd on a Monday, the 3rd on a Tuesday, the 4th on a Wednesday, the 5th on a Thursday, the 6th on a Friday, 7th on a Saturday and so on. This pattern repeats itself up to the 28th of the month (that most frequently falls on a Saturday).
Because not all months have always 29, 30 or 31 days, the pattern changes for the last three days of the month. The 29th of the month is most common on a Tuesday and Sunday, the 30th is most common on a Monday and Wednesday and finally the 31st of the month most frequently occurs on a Thursday.
The distribution of days in the calendar is not symmetrical and certain combinations are more common than others. This is a result of the aberrations in the calendar around the century years.
Whether Friday the 13th is unlucky is something this paper can’t answer. However, the 13th of the month more frequently falls on a Friday than on any other day.