The data is also provided in Q8-1.rda (the data frame is called Q8). To call the data in the console:
Q8
x y
1 3 1.20
2 4 1.40
3 5 1.60
4 6 1.75
5 7 1.85
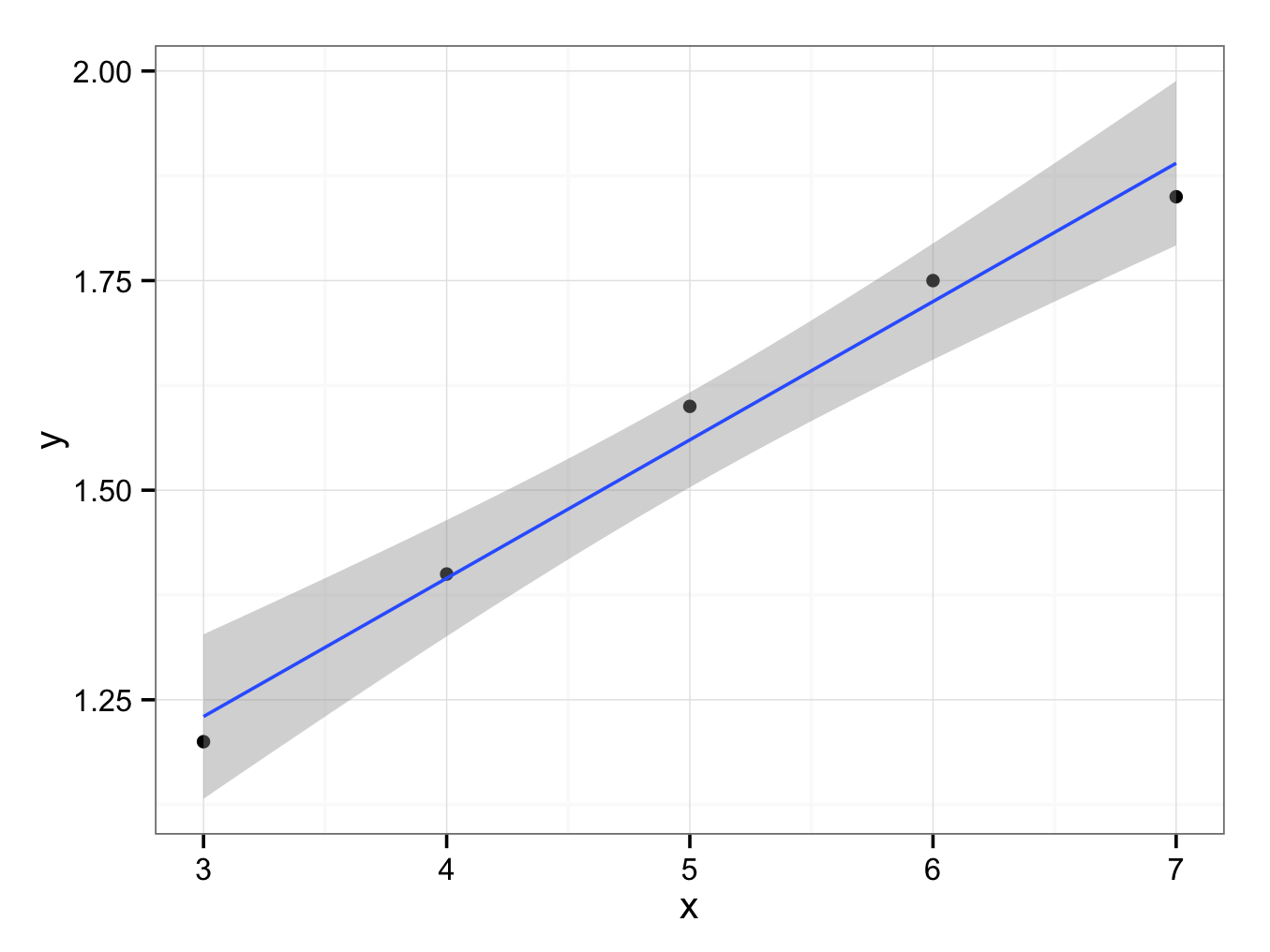
- Plot the data, draw the regression line and estimate the equation of the line:
ggplot() + geom_point(aes(x = x,y = y),data=Q8) + geom_smooth(aes(x = x,y = y),data=Q8,method = ‘lm’) + theme_bw()
Call:
lm(formula = y ~ x, data = Q8)
Coefficients:
(Intercept) x
0.735 0.165
The equation of the regression line therefore is:
y = 0.735 + 0.165 × x
- What is the correlation coefficient?
cor(Q8$x,Q8$y,method=’pearson’)
[1] 0.9913889
The correlation coefficient therefore is 99%.
- Interpolate the y-value for x = 5.5
y(x = 5.5) = 0.735 + 0.165 × 5.5 = 1.6425
- Extrapolate the y-values for x = 0.1 and x = 15
y(x = 0.1) = 0.735 + 0.165 × 0.1 = 0.7515
y(x = 15) = 0.735 + 0.165 × 15 = 3.21
The data is also provided in Q8-2.rda (the data frame is called Q8Extended). To call the data in the console:
Q8Extended
x y
1 0.1 -1.25
2 0.2 -0.70
3 1.0 0.40
4 2.0 0.90
5 3.0 1.20
6 4.0 1.40
7 5.0 1.60
8 6.0 1.75
9 7.0 1.85
10 8.0 1.95
11 9.0 2.05
12 10.0 2.10
13 12.0 2.25
14 14.0 2.35
15 15.0 2.40
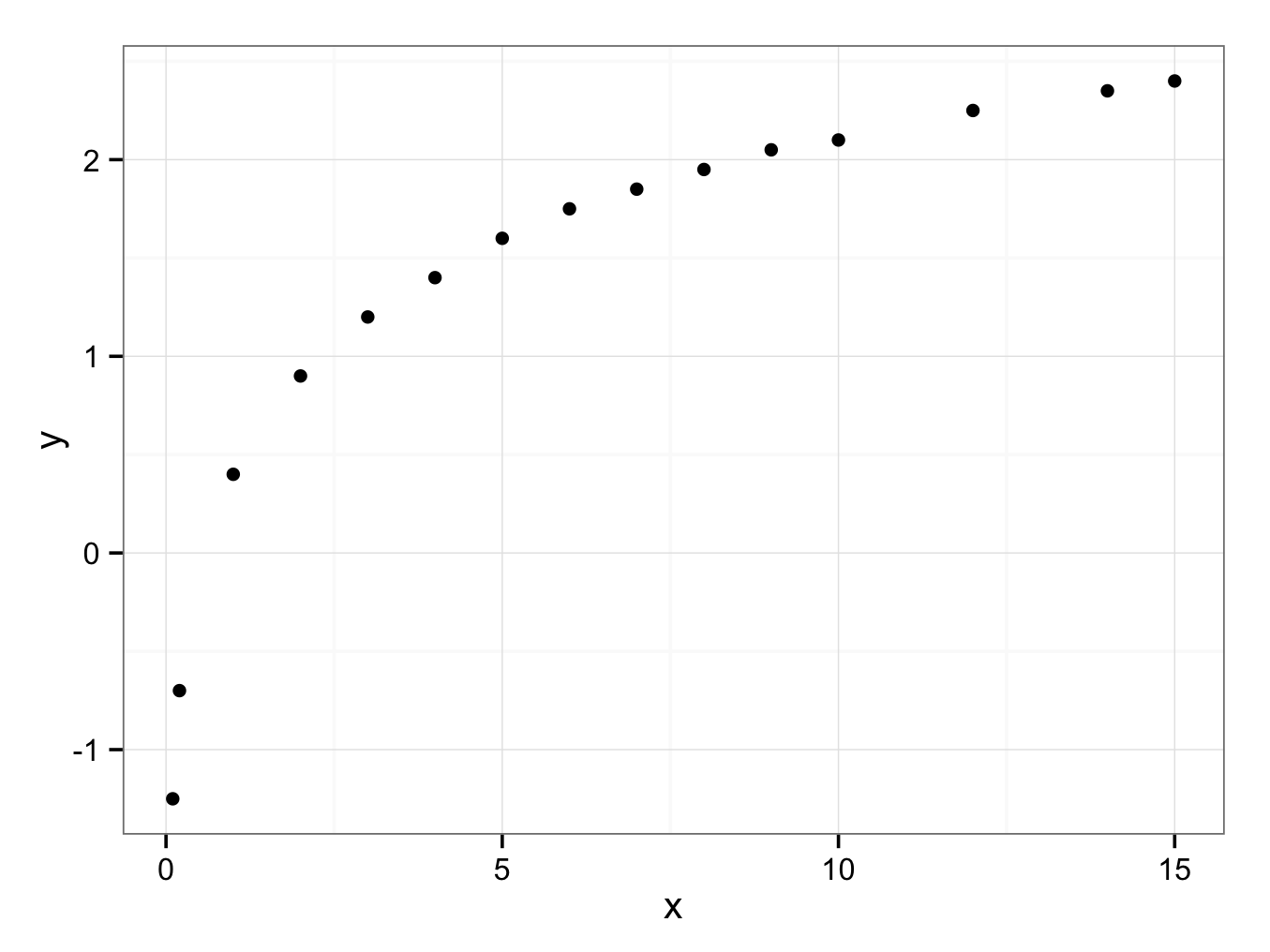
- Plot these data in a graph.
To create a scatterplot to evaluate the relation between the two variables (without a regression line):
ggplot() + geom_point(aes(x = x,y = y),data=Q8Extended)+ theme_bw()
- What is the relation between x and y and what is the value of the correlation coefficient?
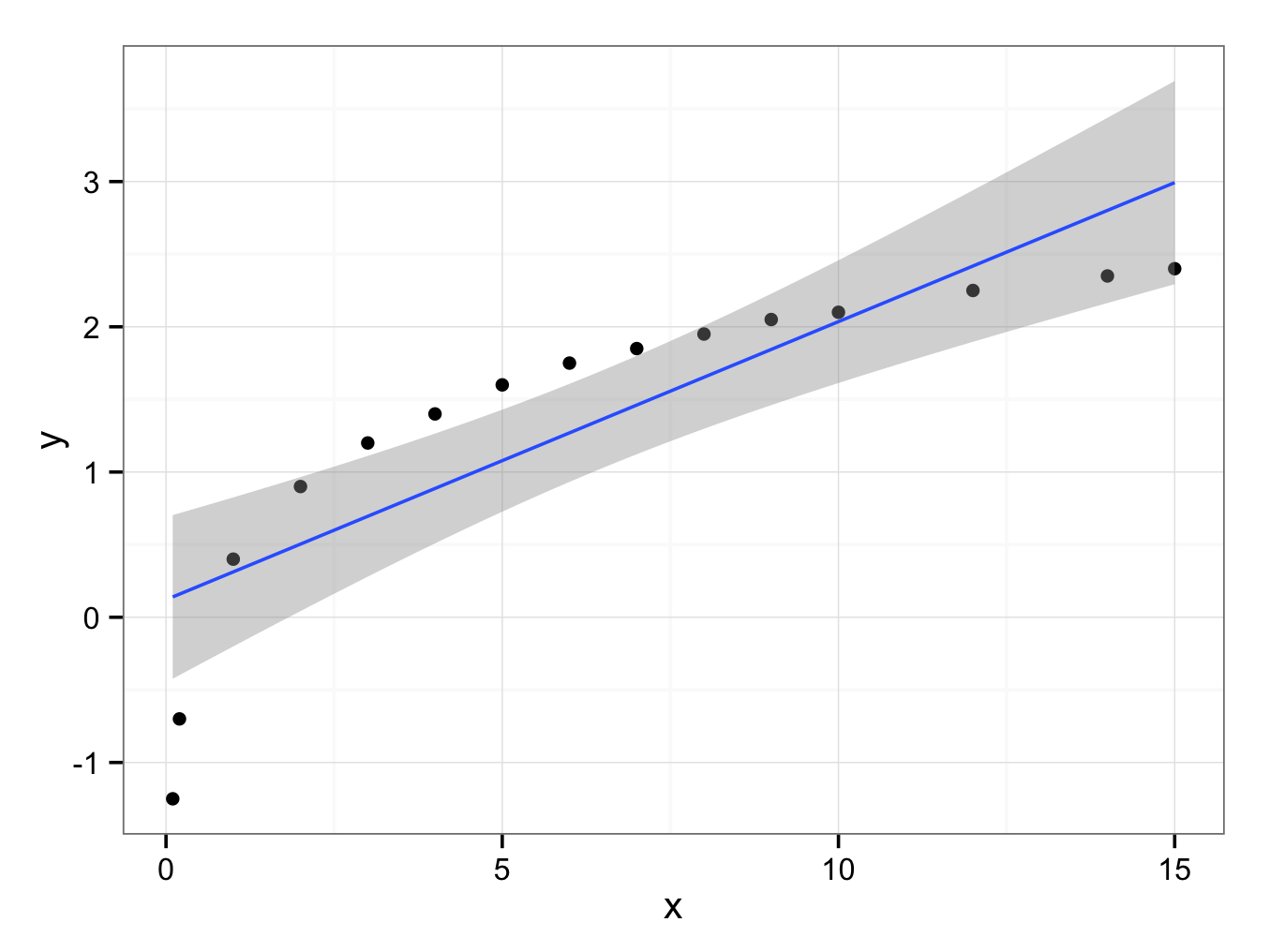
A linear regression is clearly hopeless:
ggplot() + geom_point(aes(x = x,y = y),data=Q8Extended) + geom_smooth(aes(x = x,y = y),data=Q8Extended,method = ‘lm’) + theme_bw()
 x and y appear to have a logarithmic relation and the general equation of the regression line is:
x and y appear to have a logarithmic relation and the general equation of the regression line is:
y = b + a × log(x)
or:
ggplot() + geom_point(aes(x = log(x),y = y),data=Q8Extended) + geom_smooth(aes(x = log(x),y = y),data=Q8Extended,method = ‘lm’) + theme_bw()
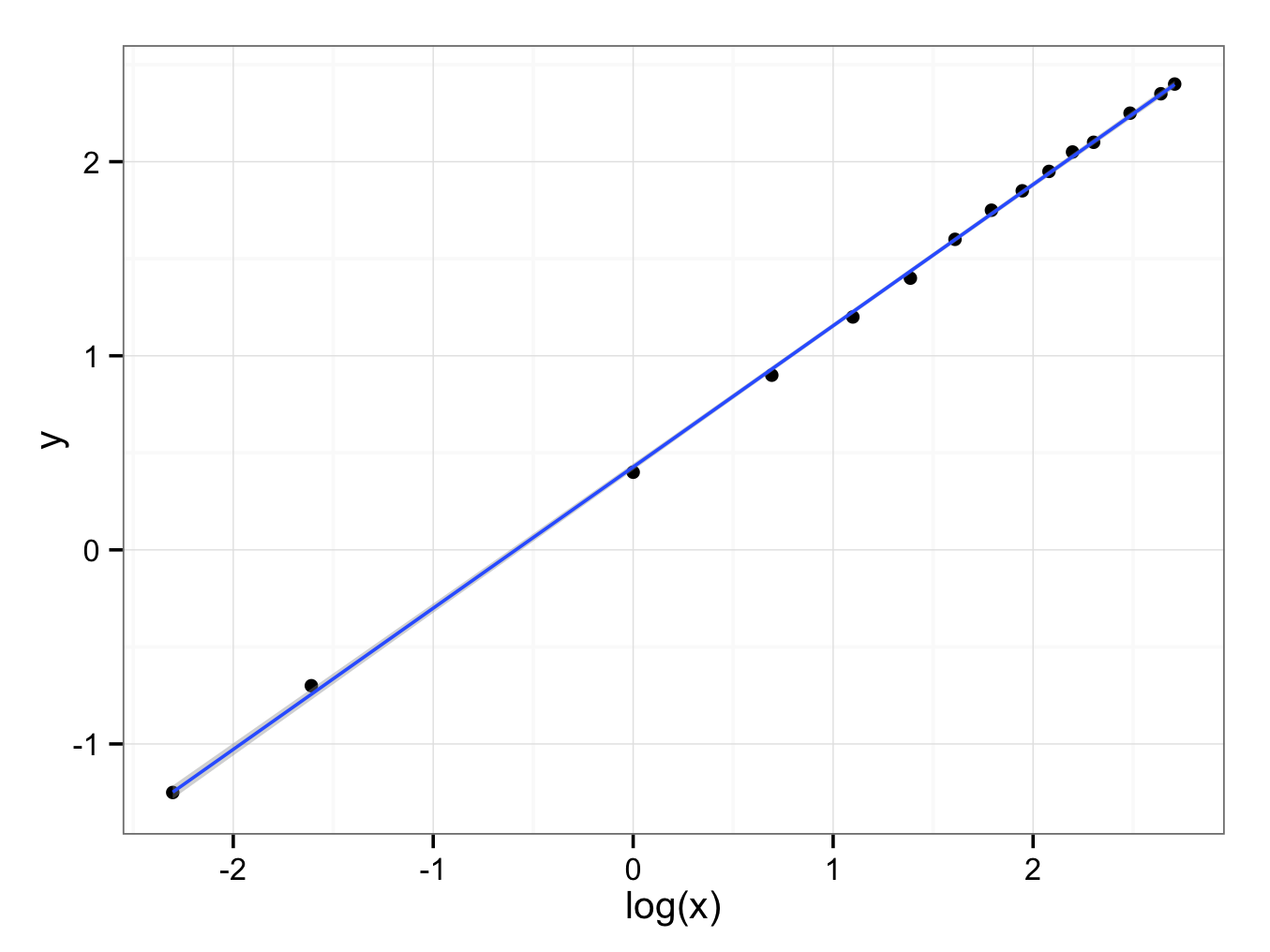 The equation of the regression line is:
The equation of the regression line is:
fit<-lm(y~log(x),data=Q8Extended)
fit
Call:
lm(formula = y ~ log(x), data = Q8Extended)
Coefficients:
(Intercept) log(x)
0.4271 0.7276
Or:
y = 0.4271 + 0.7276 × log(x)
To find the value of the correlation coefficient:
cor(log(Q8Extended$x),Q8Extended$y,method=’pearson’)
[1] 0.9997933
- What are the y-values for x = 0.1 and x = 15?
As described under 6., the equation of the regression line is:
y = 0.4271 + 0.7276 × log(x)
Therefore,
y(x = 0.1) = 0.4271 + 0.7276 × log(0.1) ≈ -1.25
y(x = 15) = 0.4271 + 0.7276 × log(15) ≈ 2.40
This question illustrates again the danger of extrapolating data!
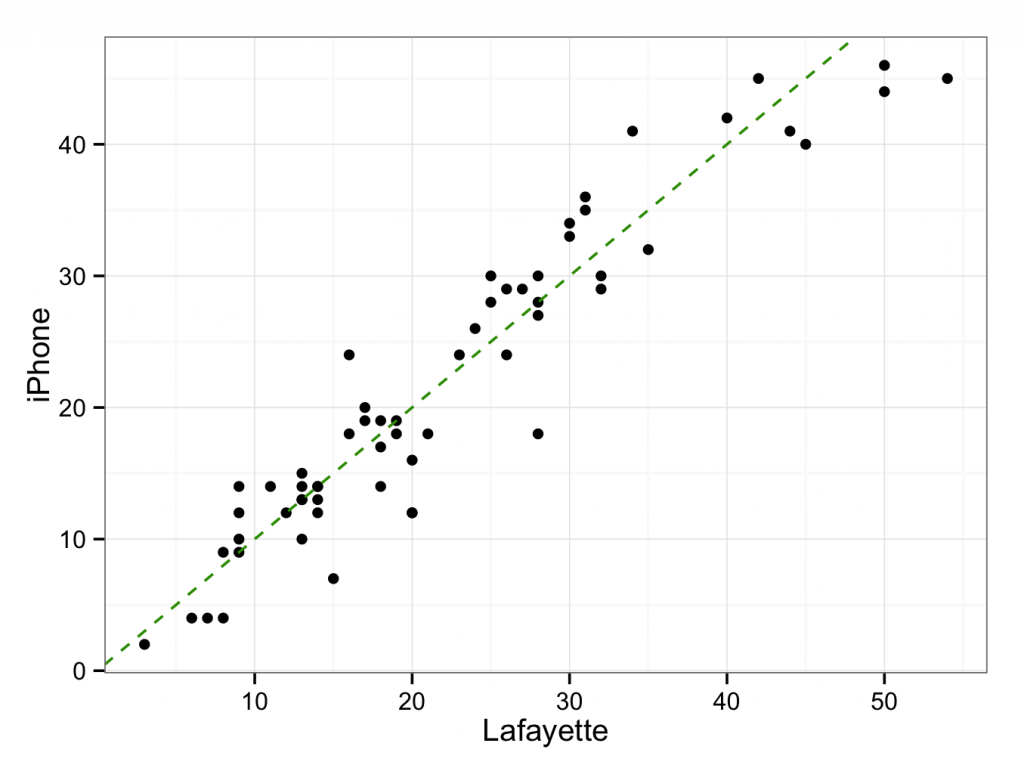
- The scatterplot and line x=y can be created in the Deducer GUI with plot builder, or the following command in the R / JGR console:
ggplot() + geom_point(aes(x = Lafayette,y = iPhone),data=goniometer) + theme_bw() + geom_abline(data=goniometer,intercept = 0.0,slope = 1.0,colour = ‘#339900′,linetype = 2)
- The Deducer GUI or the console can be used to calculate the Pearson correlation coefficient:
cor(goniometer$Lafayette,goniometer$iPhone,method=”pearson”)
[1] 0.9473263
Therefore, Pearson’s correlation coefficient is 95%.
- The Deducer GUI or the console can be used to calculate the ICC:
library(irr)
icc(goniometer,model=”twoway”,type=”agreement”)
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 60
Raters = 2
ICC(A,1) = 0.948
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(59,59.8) = 37 , p = 1.6e-31
95%-Confidence Interval for ICC Population Values:
0.914 < ICC < 0.968
Therefore, the ICC is 95%.