Essentially, a regression plot is a scatter plot with a fitted regression line. Regression lines could be linear, quadratic, and polynomial amongst others. The example below demonstrates how to create a linear regression plot for Anscombe’s first data set. Download the anscombe.rda dataset for this example 1.
Create a scatterplot as discussed:
Anscombe’s fictional data sets can be shown by:
anscombe.quartet
X1 Y1 X2 Y2 X3 Y3 X4 Y4
1 10 8.04 10 9.14 10 7.46 8 6.58
2 8 6.95 8 8.14 8 6.77 8 5.76
3 13 7.58 13 8.74 13 12.74 8 7.71
4 9 8.81 9 8.77 9 7.11 8 8.84
5 11 8.33 11 9.26 11 7.81 8 8.47
6 14 9.96 14 8.10 14 8.84 8 7.04
7 6 7.24 6 6.13 6 6.08 8 5.25
8 4 4.26 4 3.10 4 5.39 19 12.50
9 12 10.84 12 9.13 12 8.15 8 5.56
10 7 4.82 7 7.26 7 6.42 8 7.91
11 5 5.68 5 4.74 5 5.73 8 6.89
The first data set has X1 on the x -axis and Y1 on the y-axis. To create a scatterplot:
regressionplot<-ggplot() +
geom_point(aes(x = X1,y = Y1),data=anscombe.quartet) +
ggtitle(label = ‘Anscombe\’s First Data Set’) +
theme_bw()
If you are using ggplot < 0.9.2, the title can be set using: opts(title=’Anscombe\’s First Data Set’)
The backslash \ before the ‘s is required so the quotation mark does not indicate the end of the title’s text string, but that the quotation mark is part of the title!
The quotation marks may have to be re-entered if the code is copied and pasted into the console.
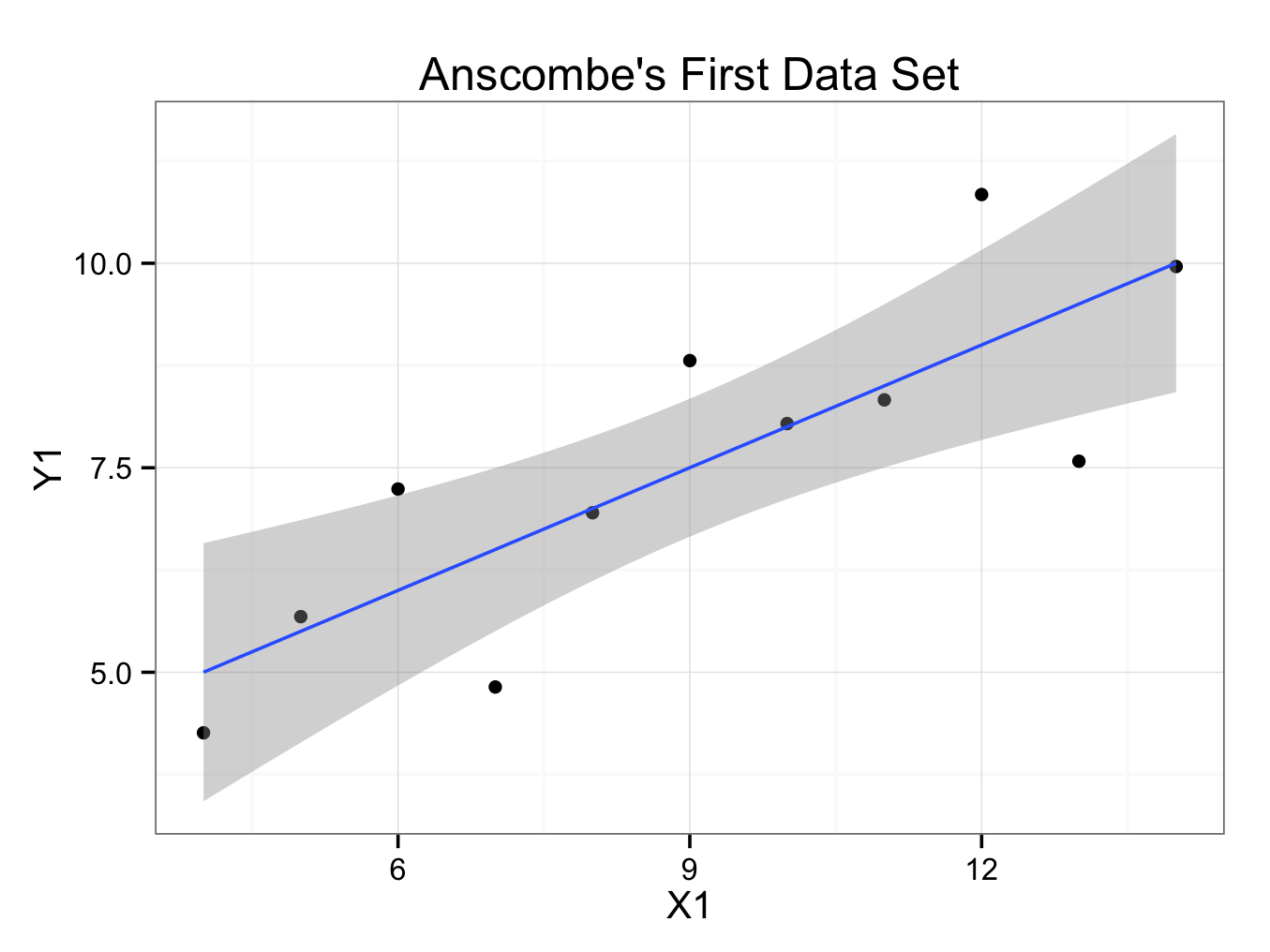
To add a regression line with a 95% confidence interval:
regressionplot<- regressionplot + geom_smooth(aes(x = X1,y = Y1),data=anscombe.quartet,method = ‘lm’)
regressionplot
Will show the plot:
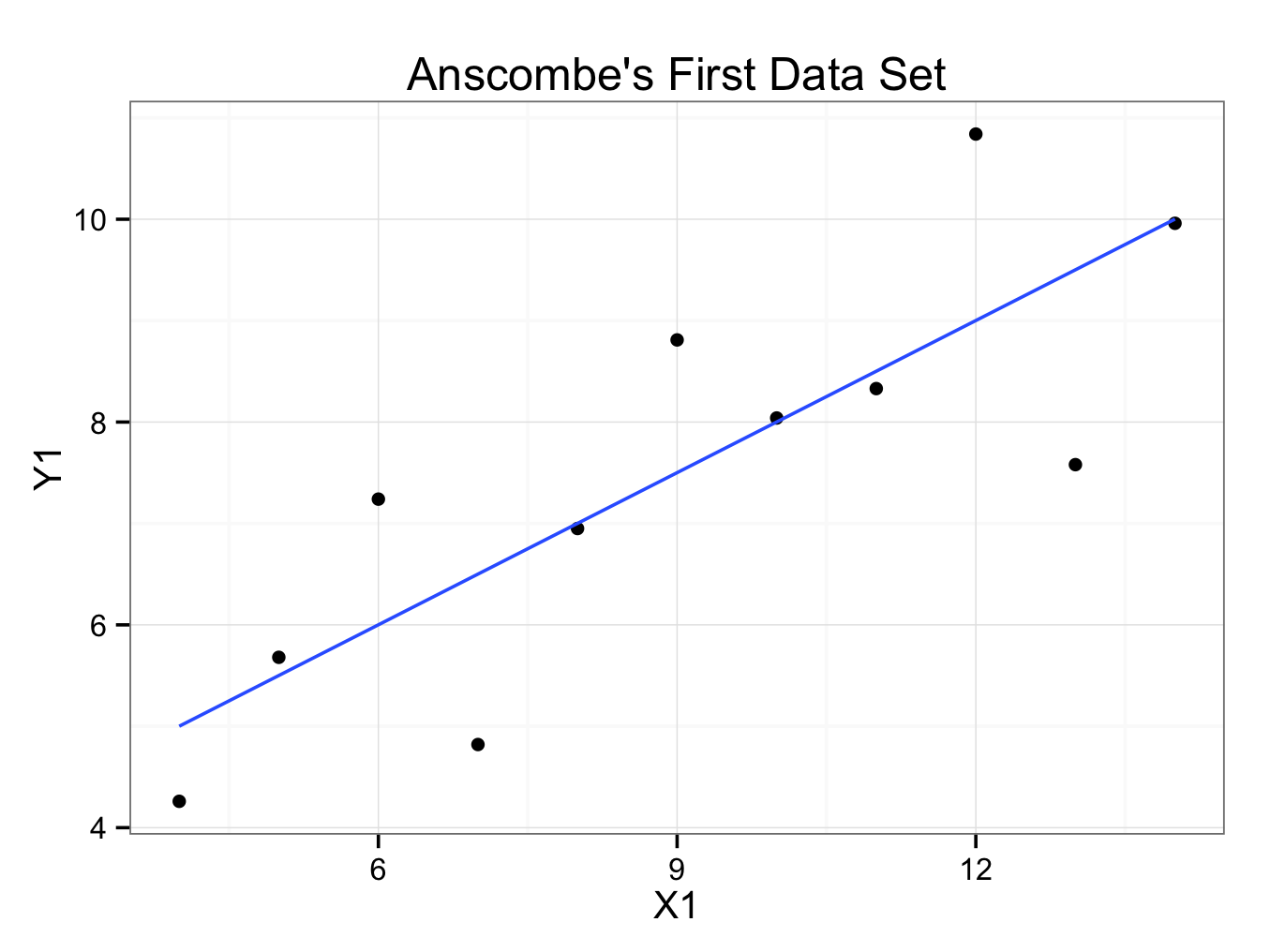
 Or without a 95% confidence interval:
Or without a 95% confidence interval:
regressionplot2<-ggplot() +
geom_point(aes(x = X1,y = Y1),data=anscombe.quartet) + geom_smooth(aes(x = X1,y = Y1),data=anscombe.quartet,method = ‘lm’, se = FALSE) +
ggtitle(label = ‘Anscombe\’s First Data Set’) +
theme_bw()
regressionplot2
Will show the plot:
It is customary to put the independent (explanatory or predictor) variable on the x-axis (abscissa) and the dependent (response or outcome) variable on the y-axis (ordinate). However, it is not always clear which variable is dependent and which independent.