Linear Discriminant Analysis(LDA) is a linear transformation technique of supervised machine learning (there needs to be a classifier). The aim of the technique is to find a linear combination of variables that separates the classifier variables as much as possible.
To illustrate the method, R’s build in data set “iris” is used. The iris data set contains the sepal and petal length and width of three different types of iris plants: Setosa, Versicolor and Virginica. Have a look at the iris data set:
head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
str(iris)
‘data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 …
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 …
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 …
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 …
$ Species : Factor w/ 3 levels “setosa”,”versicolor”,..: 1 1 1 1 1 1 1 1 1 1 …
Load the MASS package:
library(MASS)
And perform linear discriminant analysis:
lda_iris <- lda(iris$Species ~ iris[,1] + iris[,2] + iris[,3] + iris[,4])
lda_iris
Call:
lda(iris$Species ~ iris[, 1] + iris[, 2] + iris[, 3] + iris[,
4])
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Group means:
iris[, 1] iris[, 2] iris[, 3] iris[, 4]
setosa 5.006 3.428 1.462 0.246
versicolor 5.936 2.770 4.260 1.326
virginica 6.588 2.974 5.552 2.026
Coefficients of linear discriminants:
LD1 LD2
iris[, 1] 0.8293776 0.02410215
iris[, 2] 1.5344731 2.16452123
iris[, 3] -2.2012117 -0.93192121
iris[, 4] -2.8104603 2.83918785
Proportion of trace:
LD1 LD2
0.9912 0.0088
Now use the model to predict the species of each plant:
lda_iris_predict <- predict(lda_iris, iris[,1:4])
Attach this predicted variable (stored in lda_iris_predict$class) to the original iris data frame as a new variable called Predict and have a look at the top (head) of the data frame:
iris$Predict <- lda_iris_predict$class
head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species Predict
1 5.1 3.5 1.4 0.2 setosa setosa
2 4.9 3.0 1.4 0.2 setosa setosa
3 4.7 3.2 1.3 0.2 setosa setosa
4 4.6 3.1 1.5 0.2 setosa setosa
5 5.0 3.6 1.4 0.2 setosa setosa
6 5.4 3.9 1.7 0.4 setosa setosa
The values of the discriminant functions can be found by:
lda_iris_predict$x[,1] # contains the values for the first discriminant function
1 2 3 4 5 6 7 8 9 10 11
8.0617998 7.1286877 7.4898280 6.8132006 8.1323093 7.7019467 7.2126176 7.6052935 6.5605516 7.3430599 8.3973865
—
144 145 146 147 148 149 150
-6.7960192 -6.8473594 -5.6450035 -5.1795646 -4.9677409 -5.8861454 -4.6831543
lda_iris_predict$x[,2] # contains the values for the second discriminant function
1 2 3 4 5 6 7 8 9
0.300420621 -0.786660426 -0.265384488 -0.670631068 0.514462530 1.461720967 0.355836209 -0.011633838 -1.015163624
—–
145 146 147 148 149 150
2.428950671 1.677717335 -0.363475041 0.821140550 2.345090513 0.33203381
How good were the predictions? Just create a confusion table of the classifier (Species) agains the predictor (Predict):
table(iris$Species, iris$Predict)
| Setosa | Versicolor | Virginica | |
|---|---|---|---|
| Setosa | 50 | 0 | 0 |
| Versicolor | 0 | 48 | 2 |
| Virginica | 0 | 1 | 49 |
So, all Setosa species were predicted correctly. Two Versicolor species were incorrectly labelled as Virginica and one Virginica was incorrectly labelled as Versicolor. Consequently, the accuracy is:
To plot the data in ggplot:
iris_lda_df <- data.frame(first = lda_iris_predict$x[,1], second = lda_iris_predict$x[,2], Species = iris$Species, Predict = iris$Predict)
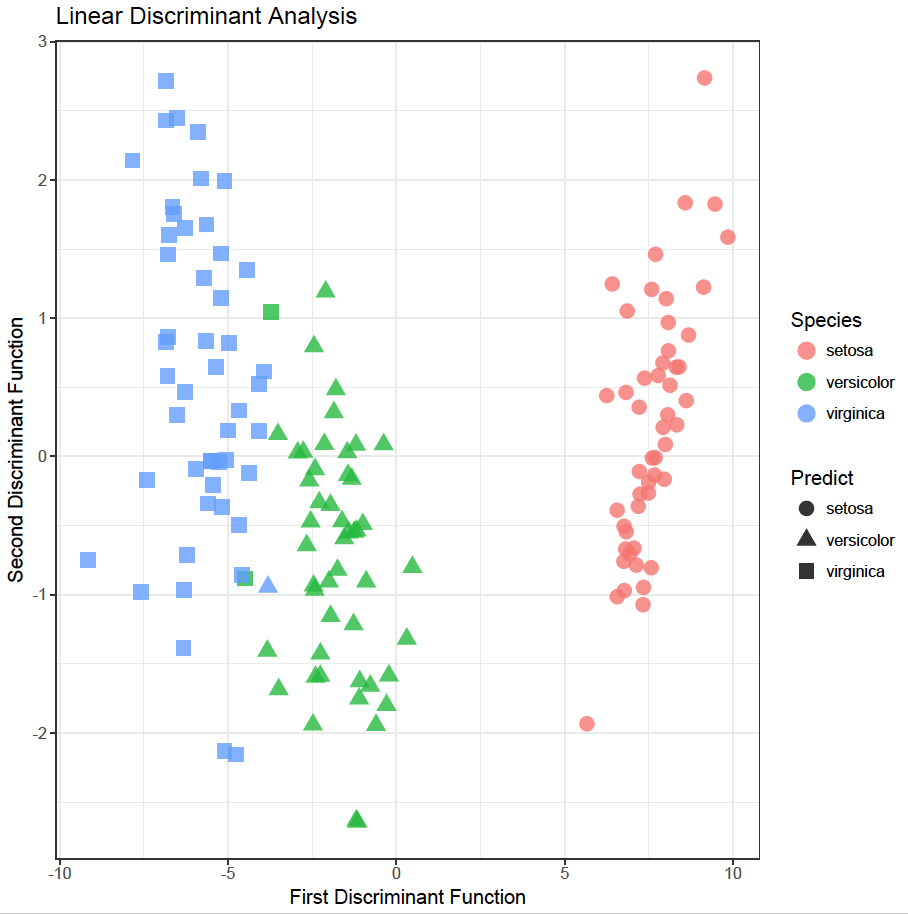
ggplot(iris_lda_df, aes(x = first, y = second, colour = Species, shape = Predict)) +
+ geom_point(size = 4, alpha = 0.8) +
+ theme_bw() +
+ ggtitle(“Linear Discriminant Analysis”) +
+ scale_x_continuous(“First Discriminant Function”) +
+ scale_y_continuous(“Second Discriminant Function”)
The plot shows the separation obtained and the classification (actual and predicted). The two green squares were predicted as Virginica, but are actually Versicolor species. Similarly, the blue triangle was predicted as Versicolor but was actually a Virginica species. Overall, a very satisfactory model!